Задание 1
Как нам известно, по теореме Виета сумма корней квадратного уравнения равна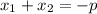 
, а их произведение: 
.
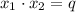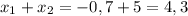. Следовательно 
.
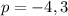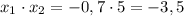. Следовательно 
.
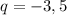Однако, в задании требуется составить квадратное уравнение с целыми коэффициентами. Значит, все показатели нужно умножить на 10. Итак, вот наше квадратное уравнение:
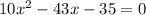
Задание 2
Как нам известно, по теореме Виета сумма корней квадратного уравнения равна 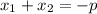, а их произведение: 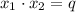. Это модификация стандартного квадратного уравнения. Поэтому 
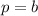, а 
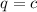. Так же мы знаем, что применение теоремы Виета возможно только в том случае, если 
(коэффициент перед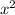 
) равен 1. Приступаем к вычислениям.
.
.
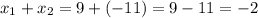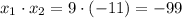Итак, вот наше квадратное уравнение:
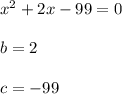
Задание 3
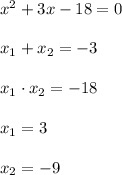
Рассмотрим функцию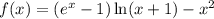 
.
Область определения функции: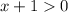 
откуда 
.
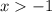Исследуем функцию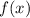 
на монотонность. Ищем производную функции
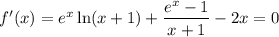
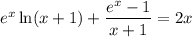
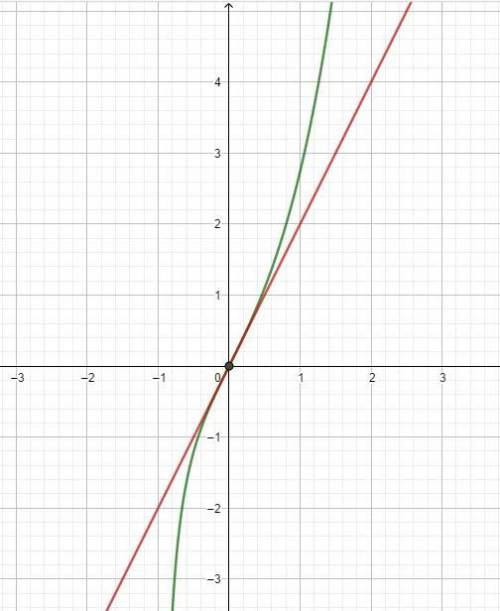
Строим график функции стоящую слева в уравнении - возрастающая (на области определения) и прямую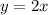 
. Графики пересекаются только в одной точке (0;0).
(-1)___-____(0)_____+____
При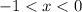 
производная отрицательная, а при 
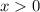- положительная. Следовательно, функция 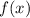на промежутке 
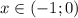убывает, а на пром. 
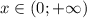- возрастает. Значит, в точке 
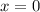функция имеет максимум, который равный 0
Следовательно, функция 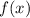всюду положительна на области определения и кроме точки 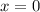, получаем
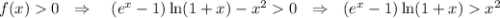
2) -184,2/(-600)=0,307
3)350,7/(-350)=-1,002
4)-0,4/100=-0,004
5)-17,64/480=-0,03675
минус на минус дает плюс
минус на плюс дает минус