Пошаговое объяснение:
Рисунок сразу с тремя графиками функций на рисунке в приложении.
В качестве исходного - график Y= cosX.
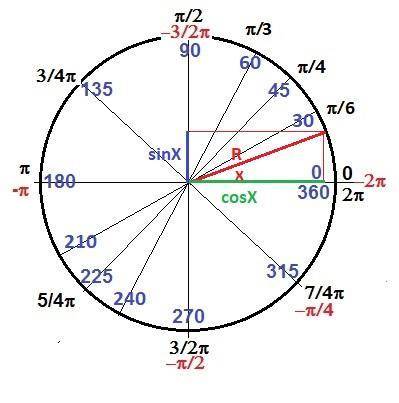
Эта функция от вращения точки по окружности радиусом = 1.
Rx/R = cosX, Ry/R = sinX. - на рисунке в приложении.
И так период функции Y = cosX = 2*π = 360°
Амплитуда значений таких функций не может быть больше R = 1.
Задание 1. Y = cos 2*x
Амплитуда остаётся такой же = 1, а вот период изменился и стал уже не 360°, а 360/2 = 180° = π.
На компьютерных графиках писать π - сложно. 30° = π/6. 60° = π/3.
СВОЙСТВА.
Амплитуда осталась равной единице, сдвига по оси Х - нет, а вот период стал в два раза меньше.
Задача 2 - Y= 1/2*cosX
Здесь совсем малое свойство - амплитуда уменьшается в два раза, па период так и остался - 2π = 360°
ДОПОЛНИТЕЛЬНО
Для построения тригонометрических функций надо запомнить значения функции в основных точках.
Х=0, У = 1
Х = π/3 = 60° У = √3/2 ≈ 0,87
Х = π/6 = 30° У = 0,5
Х = π/2 = 90° У = 0.

Пошаговое объяснение:
Рисунок сразу с тремя графиками функций на рисунке в приложении.
В качестве исходного - график Y= cosX.
Эта функция от вращения точки по окружности радиусом = 1.
Rx/R = cosX, Ry/R = sinX. - на рисунке в приложении.
И так период функции Y = cosX = 2*π = 360°
Амплитуда значений таких функций не может быть больше R = 1.
Задание 1. Y = cos 2*x
Амплитуда остаётся такой же = 1, а вот период изменился и стал уже не 360°, а 360/2 = 180° = π.
На компьютерных графиках писать π - сложно. 30° = π/6. 60° = π/3.
СВОЙСТВА.
Амплитуда осталась равной единице, сдвига по оси Х - нет, а вот период стал в два раза меньше.
Задача 2 - Y= 1/2*cosX
Здесь совсем малое свойство - амплитуда уменьшается в два раза, па период так и остался - 2π = 360°
ДОПОЛНИТЕЛЬНО
Для построения тригонометрических функций надо запомнить значения функции в основных точках.
Х=0, У = 1
Х = π/3 = 60° У = √3/2 ≈ 0,87
Х = π/6 = 30° У = 0,5
Х = π/2 = 90° У = 0.


Пошаговое объяснение:
Вопрос 1.
ВОЗРАСТАНИЕ функции - производная функции положительная.
1) y(x) = (N+5)*x - 4 - функция - график - прямая линия..
y'(x) = N+5 - производная.
Функция возрастает при N> -5.
2) y(x) = N*x³ - 5/16 - функция
y'(x) = 3*N*x² - производная
Функция возрастает при N>0.
Вопрос 2.
Чётность и нечетность.
У чётной функции все элементы должны быть четной степени (0, 2, 4...) f(-x) = f(x)
У нечётной функции - все нечетной степени Х.
А если есть показатели разной четности, то это функция общего вида - ни чётная ни нечётная.
Например:
f(x) = a*x⁴ + b*x² + c - это четная функция.
f(x) = a*x⁵ + b*x³ + c*x - нечётная функция.
РЕШЕНИЕ
1) y(x) = N*x³ + 2*N*x⁰ - общего вида.
2) y(x) = N*x² - x¹ + 3*N*x⁰ - ни чётная, ни нечётная - общего вида.