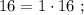
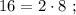
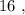т.е.: 
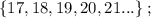
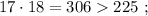
каждое – будет, очевидно, больше чем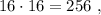 
т.е. больше 
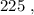а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.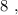
т.е.: 
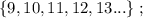
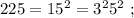
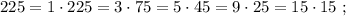
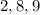и 
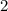и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы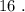 
и никаких натуральных чисел нет. и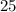 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы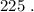 
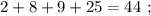
63.
Пошаговое объяснение:
Рассмотрим все пары натуральных чисел, удовлетворяющих условию m+n=16:
1) 1 и 15 взаимно простые, произведение 1•15 = 15;
2) 2 и 14 не являются взаимно простыми, (например, имеют общий делитель 2);
3) 3 и 13 взаимно простые, произведение 3•13 = 39;
4) 4 и 12 не являются взаимно простыми, (например, имеют общий делитель 2);
5) 5 и 11 являются взаимно простыми, произведение 5•11 = 55;
6) 6 и 10 не являются взаимно простыми, (например, имеют общий делитель 2);
7) 7 и 9 являются взаимно простыми, произведение 7•9= 63;
8) Пара 8 и 8 не удовлетворяет условию, слагаемые не являются взаимно простыми, (например, имеют общий делитель 2)
Остальные пары чисел будут отличаться лишь порядком следования и были рассмотрены.
Наибольшее произведение слагаемых 7 и 9 равно 7•9= 63.
х+360=3х
2х=360
х=180
во 2 день 3х=540