В январе 2016 г во время сильной снежной бури образовался опасный затор на трассе Оренбург-Орск, в котором оказались заблокированными сотни людей. Данил Максудов полицейский, попал в больницу с сильным обморожением из-за того, что отдал куртку, шапку и перчатки тем, кто больше в этом нуждался. После этого Данил еще несколько часов в пургу выводить людей из затора. Затем сам Максудов оказался в отделении экстренной травматологии с обмороженными руками, пришлось ампутировать пальцы. За проявленный героизм Данилу вручили Орден Мужества.
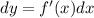 или
или 

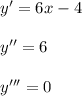


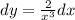
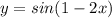




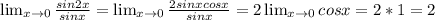
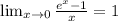
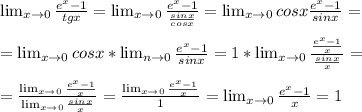
Решение
По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:
326 * 3 = 978(кирпичей);
далее вычисляем, сколько всего было кирпичей:
978 * 5 = 4890.
ответ: вначале недели каменщики получили всего 4890 кирпичей.
Задача 2
Токарь и его ученик вместе за смену выточили 130 деталей. Сколько деталей выточил каждый из них, если часть деталей, которую выточил токарь, уменьшенная в 3 раза, была равна деталям, которые выточил ученик, увеличенным в 4 раза?
Решение
Пусть ученик выточил x деталей. Тогда:
4x = (130 – x) : 3
130 – x = 4x * 3 = 12x
13x = 130
x = 130 : 13
x = 10 (деталей выточил ученик);
130 – 10 = 120 (деталей) выточил токарь.
ответ: токарь выточил 120 деталей, ученик 10.
Задача 3
Из автобуса на остановке вышло 6 пассажиров, а вошло 11. На следующей остановке вышло 8, вошло 9. Сколько пассажиров стало в автобусе, если вначале в автобусе было 24 пассажира?
Решение
1) 24 – 6 + 11 = 29 (пассажиров) стало в автобусе после первой остановки;
2) 29 - 8 + 9 = 30 (пассажиров).
ответ: в автобусе стало 30 пассажиров.
Задача 4
Из двух населенных пунктов, навстречу друг другу одновременно выехали два автомобиля. Первый может преодолеть все расстояние за 6 часов, а второй за 8 часов. Какую часть расстояние они преодолевают за 1 час?
Решение
1) 1/6 + 1/8 = 8/48 + 6/48 = 14/48 = 7/24.
ответ: за 1 час автомобили приближаются к друг другу на 7/24 всего пути.
Задача 5
От веревки длинной 48 метров отрезали 3/4 части. Какой длины стала веревка?
Решение
1) 48 : 3/4 = 36 (м) отрезали от веревки;
2) 48 – 36 = 12 (м).
ответ: веревка стала равна 12 метров.