ответ:
пошаговое объяснения: предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — . тогда формулы
параметрическое представление функции одной переменной.
пусть функция задана в параметрической форме, то есть в виде:
где функции и определены и непрерывны на некотором интервале изменения параметра . найдем дифференциалы от правых и левых частей каждого из равенств:
далее, разделив второе уравнение на первое, и с учетом того, что , получим выражение для первой производной функции, заданной параметрически:
для нахождения второй производной выполним следующие преобразования:
. найти вторую производную для функции заданной параметрически.
решение. вначале находим первую производную по формуле:
производная функции по переменной равна:
производная по :
тогда
вторая производная равна
ответ.
Пошаговое объяснение:
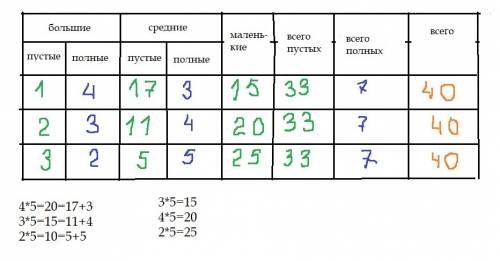
Х - пустые большие коробки
(5 - Х) ----полные большие коробки (со средними внутри)
5 * (5 - Х) = (25 - 5Х) ---- всего средних коробок в больших
У --- пустые средние коробки
((25 - 5Х) - У) --- средние коробки с маленькими внутри
5 * ( 25 - 5Х - У) = 125 - 25Х - 5У ---всего маленьких коробок ( они пустые)
33 = Х + У + 125 - 25Х - 5У --- все пустые коробки
24Х + 4У = 92
6Х + У = 33;
У = 23 - 6ХРассмотрим варианты:
1) Х = 1; У = 23-6 = 17 ;
5-1=4 больших полных; 4*5 = 20 всего средних;
(25-5-17)*5 = 15 маленьких
Всего; 5 + 20 + 15 = 40
2) Х = 2; У = 23 -12=11;
5-2=3 больших полных; 3*5 = 15 средних;
15-11 = 4 полных средних ; 4 * 5 = 20 маленьких;
Всего: 5 + 15 + 20 = 40
3) Х = 3; У = 23-18 = 5
5-3=2 больших полных; 2*5 = 10 средних
10 -5 = 5 полных средних; 5*5=25 маленьких
Всего: 5 + 10 + 25 = 40
Таким образом, при любом количестве пустых коробок среди 5 больших всего получается 40 коробок