
1) посчитаем, сколько вариантов поставить короля и ферзя:
* они занимают две подряд идущие клетки, всего вариантов 7
* мы можем еще поменять в каждом варианте КФ на ФК, получим еще 7 вариантов
итого 7+7 = 14 вариантов расстановки короля и ферзя
2) осталось шесть клеток (3 белые, 3 черные), поставим слонов:
* выберем любой цвет - 2 варианта
* выберем две клетки из трех - 3 варианта
итого 2*3 = 6 вариантов поставить слонов
3) поставим двух коней
* кони не отличаются, т.к. оба белые
* выберем из оставшихся четырех клеток две: 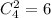
итого 6 вариантов расставить коней
4) поставим ладьи в оставшиеся клетки
итого 1 вариант для ладей
в итоге для расстановки всех фигур получим:
ответ
1. Общее решение однородного уравнения y'' - 6y' + 9y = 0
k^2 - 6k + 9 = 0
(k - 3)^2 = 0
k = 3
y = (ax + b)*e^(3x)
2. Частное решение неоднородного y'' - 6y' + 9y = 9x^2 - 12x + 2
Т.к. k <> 0, ищем y в виде px^2 + qx + r
2p - 6(2px + q) + 9(px^2 + qx + r) = 9x^2 - 12x + 2
9px^2 = 9x^2 -> p = 1
-12px + 9qx = -12x -> q = 0
2p - 6q + 9r = 2 -> r = 0
y = x^2
Общее решение: y = x^2 + (ax + b)*e^(3x)
3. Начальные условия в т. 0
y(0) = b = 1
y'(0) = 2x + 3(ax + b)*e^(3x) + a*e^(3x) = 3b + a = 3
b = 1, a = 0
y = x^2 + e^(3x)