ответ: Площадь 4,5
Дано: y = 4 - x²- парабола, y = x+2 - прямая
Найти: S=? - площадь фигуры
1) Находим точки пересечения графиков. - у1 = у2.
-x²-x+2=0 - квадратное уравнение
a = 1- верхний предел, b = -2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = 2-x- x² - подинтегральная функция - записываем в обратном порядке.
3) Интегрируем функцию и получаем:
F(x) = 2*x -1/2*x² - 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(1) = 2+-0,5-0,333 = 1,167 (1 1/6)
S(b) = S(-2) =-4+-22,667 = -3,333 (3 1/3)
S = S(a) - S(b) = 4,5 - площадь - ответ.
Рисунок к задаче в приложении.
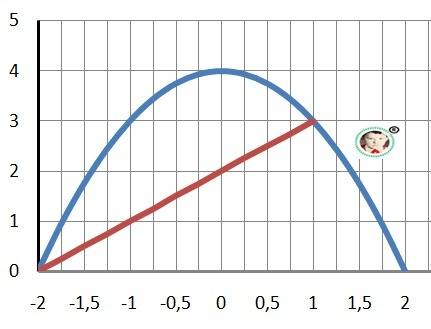
ответ: Площадь 4,5
Дано: y = 4 - x²- парабола, y = x+2 - прямая
Найти: S=? - площадь фигуры
1) Находим точки пересечения графиков. - у1 = у2.
-x²-x+2=0 - квадратное уравнение
a = 1- верхний предел, b = -2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = 2-x- x² - подинтегральная функция - записываем в обратном порядке.
3) Интегрируем функцию и получаем:
F(x) = 2*x -1/2*x² - 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(1) = 2+-0,5-0,333 = 1,167 (1 1/6)
S(b) = S(-2) =-4+-22,667 = -3,333 (3 1/3)
S = S(a) - S(b) = 4,5 - площадь - ответ.
Рисунок к задаче в приложении.

х - 1 - скорость с которой он хотел ехать сначала
30/х - время, за которое велосипедист проехал 30км
30/(х - 1) - время за которое велосипедист должен был проехать 30км
3мин = 0,05часа
Уравнение:
30/(х-1) - 30/х = 0,05
6/(х - 1) - 6/х = 1/100
600х - 600х + 600 = х² - х
х² - х - 600 = 0
D = 1 + 2400 = 2401
√D = 49
х1 = 0,5( 1 - 49) = -24 - не подходит, так как скорость не может быть отрицательной
х2 = 0,5(1 + 49) = 25
ответ: 25км/ч