вид- подлежащие выраж сущ., журавля- дополнение выраж сущ., был- сказуемое выраж гл., таким-определение выраж прил., угрожающим- сказуемое выраж прич., что- частица ,
орёл- подлежащие выраж сущ., сел-сказуемое выраж гл., в стороне - обстоятельство выраж сущ а -в- предлог., а- союз потом - обстоятельство выраж нареч., побежал - сказуемое выраж глаголом., прочь- обстоятельство выраж нареч., и- союз., взмыв в воздух- обстоятельство -взмыв- дееприч -в- предлог -воздух- сущ ., скрылся-сказуемое выраж гл., за склоном - обстоятельсво выраж сущ а -за- предлоог., горы- дополнение выраж сущ. (предлож повествов., невосклиц., сложное. сложноподч. союзное;
1 распростр., двусоставн., полное, неосложн.
2 распростр., двусоставн., полное,осложн однород скази дееприч оборотом
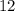(это правильно, я тоже Сириус решаю)
Пошаговое объяснение:
Пронумеруем числа 
, 
, 
, ..., 
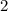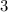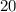
Пусть 
- ая группа состоит из чисел с номерами 
, 
, 
, ..., 
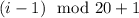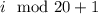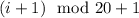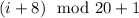(здесь 
- взятие остатка, 
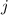- ое число в - ой группе имеет номер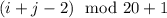 
, 
, 
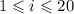). К примеру:
1-ая группа: числа , , ..., 
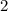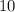
2-ая группа: числа , , ...,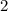 
...
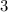20-ая группа: числа , , ...,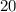 
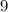
Пусть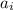 
- сумма чисел в - ой группе. Поскольку все числа целые, их сумма будет также целая, значит, ![\forall i\in[1,~20]](/tpl/images/2025/8085/f00d2.png)
: 
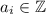. Заметим, что сумма всех чисел является суммой чисел в -ой и в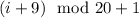 
, значит, 
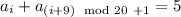. Если 
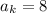, то есть ![\forall i\in [1,~k)\cup(k,20]](/tpl/images/2025/8085/cb834.png)
: 
⇒
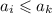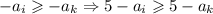. Поскольку 
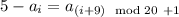и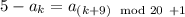 
, постольку 
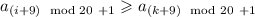. Поэтому 
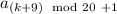- минимальное число (все остальные числа не меньше 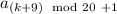(а именно все, потому что в виде 
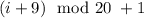представляются все числа от 1 до 20 при ![i\in[1,~20]](/tpl/images/2025/8085/a631f.png)
) ). А также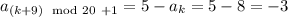 
. В итоге : 
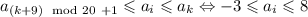. В итоге, поскольку : ![a_i\in \mathbb{Z} ~\wedge~a_i\in[-3,~8]](/tpl/images/2025/8085/54ef8.png)
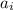, у есть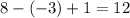 
вариантов значения. Значит, не более 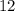сумм различны. Для полноты картины стоило бы привести пример, но это слишком просто.
