
ответ: x∈[-2;4].
Пошаговое объяснение:
1) Составляем выражение для отношения a(n+1)/a(n), где a(n+1) и a(n) - соответственно n+1 - й и n - ный члены ряда: a(n+1)/a(n)=(x-1)*(3*n-1)²/[3*(3*n+2)²].
2) Составляем выражение для модуля этого отношения. Так как (3*n-1)²>0 и 3*(3*n+2)²>0, то /a(n+1)/a(n)/=/x-1/*(3*n-1)²/[3*(3*n+2)²].
3) Находим предел этого выражения при n⇒∞: lim /a(n+1)/a(n)/=1/3*/x-1/, так как lim (3*n-1)²/[3*(3*n+2)²]=1/3.
4) Составляем и решаем неравенство 1/3*/x-1/<1. Оно имеет решение -2<x<4, то есть x∈(-2;4). Поэтому -2<x<4 - интервал сходимости ряда.
5) Остаётся исследовать поведение ряда на концах этого интервала.
а) если x=-2, то ряд принимает вид (-1)^n/[(3*n-1)²]. Так как /(-1)^n/[(3*n-1)²]/=1/[(3*n-1)²]<1/n², а ряд обратных квадратов сходится, то в точке x=-2 данный ряд тоже сходится, причём - абсолютно.
б) если x=4, то ряд принимает вид 1/[(3*n-1)²]. Как только что было показано, данный ряд сходится - значит, данный ряд сходится и в этой точке. Поэтому областью сходимости ряда является интервал x∈[-2;4].
В уравнении гиперболы разделим обе части уравнения на 225:
(9x²/225) - (25y²/225) = 225/225,
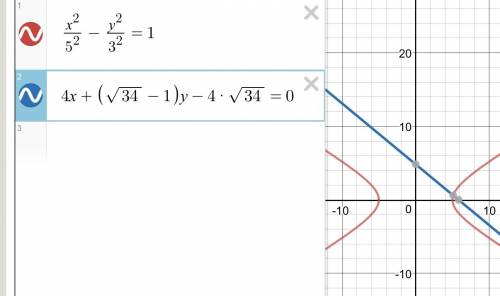
(x²/25) - (y²/9) = 1,
(x²/5²) - (y²/3²) = 1 это каноническое уравнение гиперболы, из которого определяем параметры полуосей:
а = 5 и b = 3.
Тогда полуфокусное расстояние с равно:
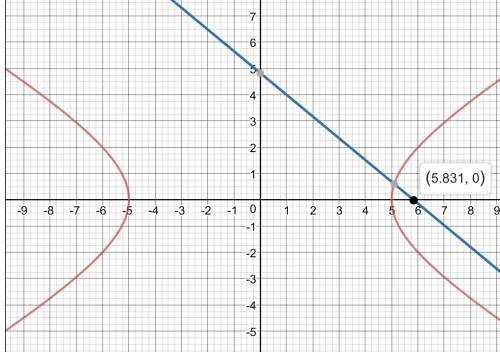
с = √(a² + b²) = √(25 + 9) = √34 ≈ 5,830952.
Отсюда определяем координаты правого фокуса гиперболы.
F(√34; 0).
Точка М(1; 4).
Находим уравнение прямой MF.
FM: (x-1)/((√34)-1) = (y-4)/(-4) это каноническое уравнение прямой,
y = (-4/((√34)-1))*x + (4√34)/((√34)-1) это оно же с угловым коэффициентом,
4x + ((√34)-1)y - 4√34 = 0 общее уравнение.