1. Метод исключения неизвестных.
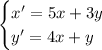
Продифференцируем первое уравнение:
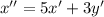
Подставим выражение для y':
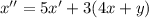
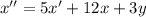
Из получившегося уравнения отнимем первое уравнение системы:
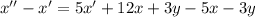
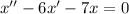
Составим характеристическое уравнение:
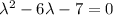
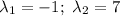
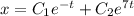
Найдем производную:
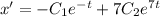
Выразим из первого уравнение системы у:
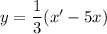
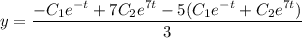
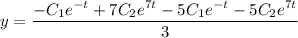
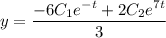
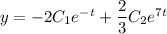
Общее решение:
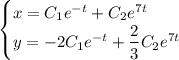
Находим решение задачи Коши:
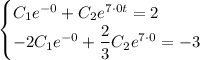
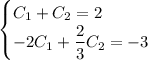
Первое уравнение домножим на 2:
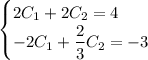
Сложим уравнения:
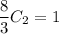
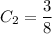
Выразим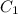 
:
Частное решение:
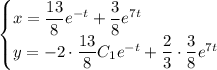
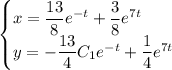
2. Метод характеристических уравнений (метод Эйлера).
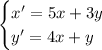
Матрица из коэффициентов при неизвестных:
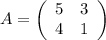
Характеристическая матрица:
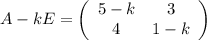
Характеристическое уравнение:
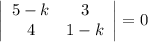
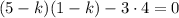
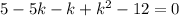
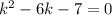
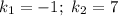
Общее решение:
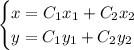
Ищем фундаментальную систему решений:
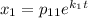
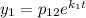
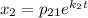
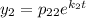
Для нахождения чисел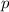 
составим систему:
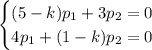
Для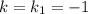 
:
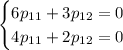
Оба уравнения дают:
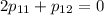
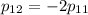
Найдем ненулевое решение. Пусть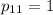 
. Тогда 
.
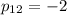Для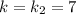 
:
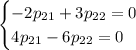
Оба уравнения дают:
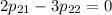
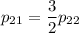
Найдем ненулевое решение. Пусть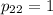 
. Тогда 
.
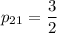Фундаментальная система решений найдена:
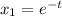
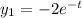
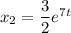
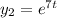
Общее решение:
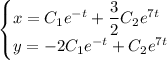
Находим частное решение:
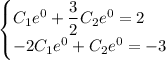
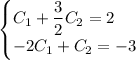
Первое уравнение домножим на 2:
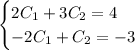
Сложим уравнения:
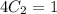
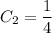
Выразим :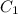
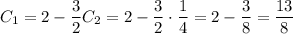
Частное решение:
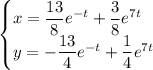
ответ: b = (-3,6,6), b (3; -6; -6), α = -60⁰
Пошаговое объяснение:
Дан вектор a(-1;2;2). Найдите координаты вектора b, коллинеарного вектору a, если a·b = 27.
Скалярное произведение векторов а и b определяется как произведение длин этих векторов на косинус угла между ними!
Поскольку векторы коллинеарные, то угол между ними равен 0 градусов, т. е косинус угла равен 1.
Длина вектора a равна
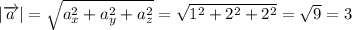
По условию задания скалярное произведение векторов равно 27
Зная длину вектора а найдем длину вектора b
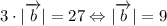
Поскольку вектора а и b коллинеарны, то и координаты связаны уравнением
Подставим координаты вектора а
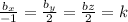
Запишем координаты вектора b через новую переменную k bx = -k, by =2k, bz = 2k
b = (-k,2k,2k)
Определим длину вектора и по теореме Пифагора
Так как длину вектора b мы знаем из скалярного произведения то
3|k| = 9
k₁ = 3 k₂=-3
Получили два варианта вектора b
Для k = 3
b = (-3,6,6)
Для k = -3
b (3; -6; -6)
Найдем угол между векторами a и c из формулы скалярного произведения, если a*c = -6; c = 4
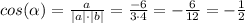
α = arccos(-0,5) = -60⁰
