Домножим все на 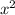 . Мы можем это сделать по причине того, что
. Мы можем это сделать по причине того, что 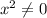 (в противном случае это давало бы ноль в знаменателе) и
(в противном случае это давало бы ноль в знаменателе) и 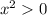 (квадрат выражения не может быть отрицательным).
(квадрат выражения не может быть отрицательным).
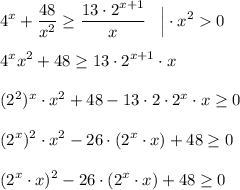
Замена: 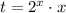 (
(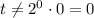 ).
).
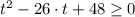
Вс уравнение 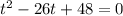 можно решить теоремой Виета:
можно решить теоремой Виета:
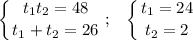
Так как перед нами парабола, ветви которой направлены вверх (по коэффициенту  ), то
), то ![t \in ( - \infty ; 0 ) \cup (0; 2 ] \cup [24; + \infty )](/tpl/images/1358/8646/4ea75.png) (точку
(точку  убираем из решения из-за ОДЗ).
убираем из решения из-за ОДЗ).
![2^x \cdot x \in ( - \infty ; 0 ) \cup (0; 2 ] \cup [24; + \infty )](/tpl/images/1358/8646/bf7b6.png) .
.
Заметим, что значение функции, задающейся уравнением 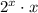 , при
, при 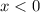 всегда будет меньше ноля (так как
всегда будет меньше ноля (так как 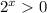 и
и 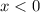 ). То есть,
). То есть, 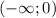 принадлежит множеству решений уравнения.
принадлежит множеству решений уравнения.
Если же  (точка
(точка 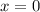 не рассматривается, так как не входит в ОДЗ), то функция
не рассматривается, так как не входит в ОДЗ), то функция 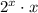 монотонно возрастает на рассматриваемом промежутке (как произведение двух положительных монотонно возрастающих функций). Следовательно, если при
монотонно возрастает на рассматриваемом промежутке (как произведение двух положительных монотонно возрастающих функций). Следовательно, если при 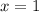 достигается крайняя точка на промежутке
достигается крайняя точка на промежутке ![(0;2]](/tpl/images/1358/8646/9ec34.png) , то при
, то при  принадлежит рассматриваемому промежутку (
принадлежит рассматриваемому промежутку (![(0;2]](/tpl/images/1358/8646/9ec34.png) ), а при
), а при  - не принадлежит. Значит, второй промежуток - это
- не принадлежит. Значит, второй промежуток - это ![(0;1]](/tpl/images/1358/8646/3ae98.png) .
.
Аналогично и рассмотрение функции 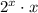 на промежутке
на промежутке 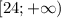 . В силу монотонности функции при положительных
. В силу монотонности функции при положительных  , при
, при 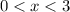 она меньше
она меньше  (что нам не подходит), а при
(что нам не подходит), а при 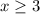 располагается в нужном промежутке.
располагается в нужном промежутке.
Значит, ![x \in ( - \infty; 0) \cup (0; 1] \cup [3; + \infty )](/tpl/images/1358/8646/2b11a.png) .
.
![\large \boxed { x \in ( - \infty; 0) \cup (0; 1] \cup [3; + \infty ) }](/tpl/images/1358/8646/871af.png)
Решите неравенство Log_(1 +1/(x+1)²) ( x²+3x +2)/(x²-3x+4) ≤ 0
ответ: x ∈ ( -∞ ; -2) ∪ (-1 ; 1/3] .
Пошаговое объяснение: x²-3x+4 =(x -3/2)² +7/4 > 0 || ≥7/4 ||
ОДЗ: { x²+3x +2 > 0 ; x+1 ≠0 . ⇔{ (x +2)(x+1) > 0 ; x ≠ - 1. ⇒
x ∈ ( - ∞ ; -2) ∪ (-1 ; ∞) .
1 +1/(x+1)² > 1 ;
Log_(1 +1/(x+1)²) ( x²+3x +2)/(x²-3x+4) ≤ 0 ⇔ 0 < ( x²+3x +2)/(x²-3x+4) ≤ 1 ⇔
0 < x²+3x +2 ≤ x²-3x+4 ⇔0 ⇔ { x²+3x +2>0 ; x²+3x +2 ≤ x²-3x+4.⇔
{ (x+2)(x+1)>0 ; x²+3x +2 ≤ x²-3x+4.⇔ { (x+2)(x+1)>0 ; x ≤ 1/3. ⇒
x ∈ ( -∞ ; -2) ∪ (-1 ; 1/3] .
Площадь поверхность находим: (15^2)*6=1350. Площадь куба находим по формуле: 6*H^2.
Объем куба равен: 15^3=3375. Объем куба равен: a^3.