А=5, Б=5, В=5, Г=5, Д=3
15 = 5+5+5=А+Б+С
13=5+5+3 = А+Г+Д
из карточек А Б В можно составить 6 троек (3*2*1=6)
АБВ, АВБ, БВА, БАВ, ВАБ, ВБА
555, 555, 555, 555, 555, 555
сумма цифр в каждой тройке =5+5+5=15
из карточек В Г Д можно составить 6 троек (3*2*1=6)
ВГД, ВДГ, ГДВ, ГВД, ДВГ, ДГВ
553, 535, 535, 553, 355, 355
сумма цифр в каждой тройке = 5+5+3=13
6 троек +6 троек =12 троек
Вывод: 10 троек, можно составить из чисел А=5, Б=5, В=5, Г=5, Д=3
вариант 2 -- числа на карточках НЕ могут повторяться
А=8, Б=2, В=5, Г=7, Д=1
15=8+2+5 = А+Б+В
13=5+7+1 = В+Г+Д
из карточек А Б В можно составить 6 троек (3*2*1=6)
АБВ, АВБ, БВА, БАВ, ВАБ, ВБА
825, 852, 258, 285, 582, 528
сумма цифр в каждой тройке = 8+2+5=15
из карточек В Г Д можно составить 6 троек (3*2*1=6)
ВГД, ВДГ, ГДВ, ГВД, ДВГ, ДГВ
571, 517, 715, 751, 157,175
сумма цифр в каждой тройке = 7+1+5=13
6 троек + 6 троек = 12 троек
Вывод: 10 троек, можно составить из чисел А=8, Б=2, В=5, Г=7, Д=1
ответ: А=5, Б=5, В=5, Г=5, Д=3 -- если числа могут повторяться
А=8, Б=2, В=5, Г=7, Д=1 -- если числа НЕ могут повторяться
57
Пошаговое объяснение:
С следующего свойства параллелограмма задача решается просто:
Диагонали параллелограмма делят его на два равных треугольника.
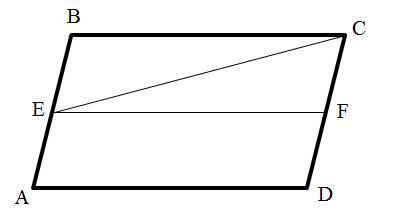
Дано: точка E середина стороны AB. Пусть точка F середина стороны CD (см. рис). Тогда отрезок EF делит параллелограмм ABCD на два равных параллелограмма AEFD и EBCF с площадью равной 76:2=38. А диагональ EC делит EBCF на два равных треугольника ECF и EBC с площадью равной 38:2=19.
А трапеция DAEC делится на части: параллелограмм AEFD и треугольник ECF. Поэтому
площадь DAEC = площадь AEFD + площадь ECF = 38 + 19 = 57.
1 вариант. 1-ый дружит только с 32-ым, 2-ой с 31-ым и 32-ым, и т.д.
Номер каждого означает, со сколькими людьми он дружит.
1 - 32
2 - 31, 32
3 - 30, 31, 32
4 - 29, 30, 31, 32
5 - 28, 29, ..., 32
6 - 27, 28, ..., 32
7 - 26, 27, ..., 32
8 - 25, 26, ..., 32
9 - 24, 25, ..., 32
10 - 23, 24, ..., 32
11 - 22, 23, ..., 32
12 - 21, 22, ..., 32
13 - 20, 21, ..., 32
14 - 19, 20, ..., 32
15 - 18, 19, ..., 32
16 - 17, 18, ..., 32
17 - Сережа, 16, 18, 19, ..., 32
18 - Сережа, 15, 16, 17, 19, ..., 32
И так далее до 32-го.
31 - Сережа, 2, 3, 4, ..., 30, 32
32 - Сережа, 1, 2, 3, ..., 31
Таким образом, получилось, что Сережа дружит со всеми от 17-го до 32-го, то есть с 16 одноклассниками..
2 вариант - 1-ый не дружит ни с кем, тогда 2-ой только с 32-ым, а 32-ой со всеми, кроме 1-го. Номер каждого на 1 больше количества его друзей.
1 - 0
2 - 32
3 - 31, 32
4 - 30, 31, 32
5 - 29, 30, 31, 32
6 - 28, 29, ..., 32
7 - 27, 28, ..., 32
8 - 26, 27, ..., 32
9 - 25, 26, ..., 32
10 - 24, 25, ..., 32
11 - 23, 24, ..., 32
12 - 22, 23, ..., 32
13 - 21, 22, ..., 32
14 - 20, 21, ..., 32
15 - 19, 20, ..., 32
16 - 18, 19, ..., 32
17 - Сережа, 18, 19, ..., 32
18 - Сережа, 16, 17, 19, 20, ..., 32
И так далее до
31 - Сережа, 3, 4, 5, ..., 30, 32
32 - Сережа, 2, 3, 4, ..., 31
И опять получилось, что Сережа дружит со всеми от 17-го до 32-го,
то есть с 16 одноклассниками.
ответ: У Сережи в любом случае 16 друзей.