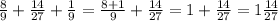
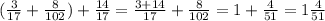
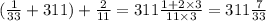
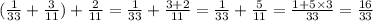
Відповідь:
Покрокове пояснення:
В Средние века солнечные часы могли выглядеть неожиданно. На площади, опираясь на косу стояла скульптура старухи-смерти, а древко ее косы являлось гномоном горизонтальных часов.
Разновидности солнечных часов были весьма многообразны. Кроме горизонтальных часов, греки имели еще и более совершенные вертикальные солнечные часы, так называемые гемоциклы, которые они располагали на общественных зданиях.
Были и зеркальные солнечные часы, которые отражали солнечный луч зеркалом на циферблат, расположенный на стене дома.
Солнечные часы встречались не только в виде часов, расположенных на открытом воздухе – на земле . колоннах и т.п., но и в виде небольших настольных часов.
Приблизительно в начале XVI в. появились оконные солнечные часы. Они были вертикальными, и их циферблатом была поверхность окна храма или ратуши. Циферблат этих часов, встречающихся довольно часто в Германии и в Англии, обычно состоит из мозаичной филенки, залитой свинцом. Прозрачная шкала позволяла наблюдать время, не выходя из здания.
ответ: 1) sin^2(a), 2) sin^2(b)
Пошаговое объяснение:
1) tg(x) и ctg(x) взаимно обратные функции, ибо tg(x) = sin(x)/cos(x), а ctg(x) = cos(x)/sin(x). Значит их произведение равно единице, т.е. tg(x)*ctg(x) = 1. Итого получаем 1-cos^2(a). Из основного тригонометрического тождества (sin^2(a)+cos^2(a) = 1) приводим полученное 1-cos^2(a) => sin^2(a) + cos^2(a) - cos^2(a) = sin^2(a)
2) Рассмотрим выражение в скобке. cos^2(b)-1=cos^2(b)-sin^2(b)-cos^2(b)=-sin^2(b). Далее умножаем на ctg^2(b). Получаем cos^2(b)*(-sin^2(b))/sin^2(b)=-cos^2(b). Далее -cos^2(b)+1=sin^2(b)
б)
в)
г)