 — неоднородное дифференциальное уравнение третьего порядка с постоянными коэффициентами
— неоднородное дифференциальное уравнение третьего порядка с постоянными коэффициентами
Принцип суперпозиции решений
Общее решение такого уравнения: 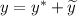 , где
, где 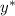 — общее решение соответствующего однородного уравнения,
— общее решение соответствующего однородного уравнения, 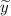 — частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
— частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
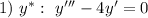
Метод Эйлера: 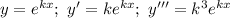
Характеристическое уравнение: 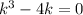
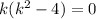
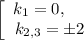
Фундаментальная система решений:
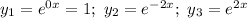
Общее решение: 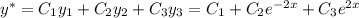
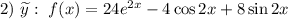
Здесь 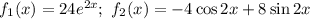
Контрольные числа: 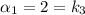 — является корнем характеристического уравнения;
— является корнем характеристического уравнения; 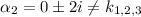 — не является корнем характеристического уравнения;
— не является корнем характеристического уравнения;
Тогда 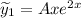 и
и 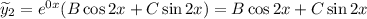
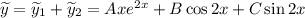
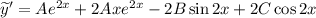
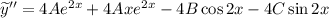
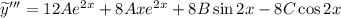
Находим неизвестные коэффициенты 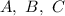 методом неопределенных коэффициентов:
методом неопределенных коэффициентов:
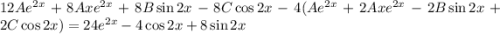
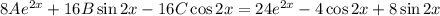
Коэффициенты около 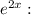
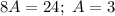
Коэффициенты около 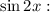
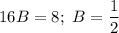
Коэффициенты около 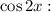
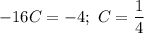
Таким образом, 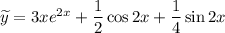
Общее решение заданного уравнения:
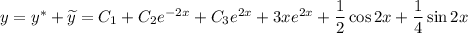
ответ: 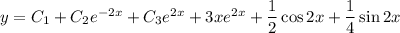
p= a+b+2c p= 2h+2c подставим p=2*9+2*12 отсюда p = 42