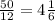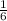, 
нам "говорит" о том, что это следующий подъезд, 4 подъезда по 12 квартир получается 48, а т.к. Глеб живет в 50 квартире, то это уже сдедующий подъезд, т.е. 5. А т.к. квартир на каждом этаже по 3, то следовательно получаем те 2 квартиры, которые остались находятся на 1 этаже. ответ: Глеб живет в 5 подъезде на 1 этаже
А = 1 1 -1
8 3 -6
4 1 -3
В = 1
2
3
находим детерминант матрицы А:
det(A)=1·3·(-3) + 1·(-6)·4 + (-1)·8·1 - (-1)·3·4 - 1·(-6)·1 - 1·8·(-3) = -9 - 24 - 8 + 12 + 6 + 24 = 1
после этого необходимо составить матрицу алгебраических дополнений. пример нахождения А11 и А12
M11 = 3 -6
1- 3 = 3·(-3) - 1·(-6) = -9 + 6 = -3
A11 = (-1)^1+1 * M11 = -3
M12 = 8 -6
4 -3 = 8·(-3) - 4·(-6) = -24 + 24 = 0
A12 = (-1)^1+2 M12 = 0
очень важно, степень образуется путем m+n, m - номер строки элемента, n - номер стоблца элемента.
(так для каждого элемента)
после располагаем их в таком порядке:
А11 А21 А31
А12 А22 А32
А13 А23 А33
и приводим это к обратной матрице, умножая каждый элемент на 1/det(A)
и последний шаг - умножаем полученную обратную матрицу на матрицу В.
ответ должен получится следующий: x1 = -8, x2 = -4, x3 = -13