Пошаговое объяснение:
Точка 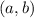 на комплексной плоскости изображает число
на комплексной плоскости изображает число 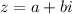
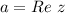 - действительная часть числа (Real)
- действительная часть числа (Real)
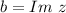 - мнимая часть числа (Imaginary)
- мнимая часть числа (Imaginary)
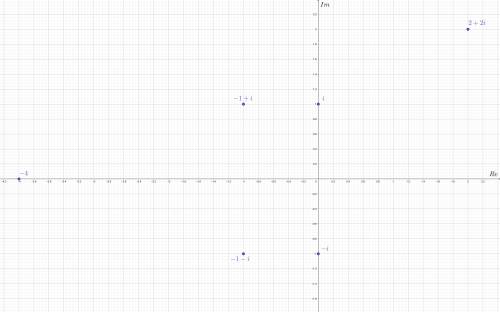
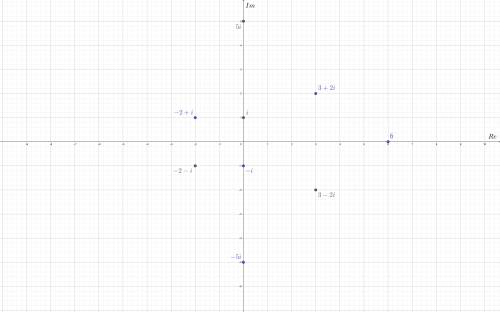
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа 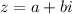 будет являться число
будет являться число 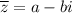 .
.
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси 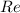 ).
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
около 29% от цены в июне и 35% от начальной цены (Советую задать вопрос : "От чего считать %?")
Пошаговое объяснение:
18 000 - начальные 100%
18 000 : 100 = 180 р - 1%
20 * 180 = 3600 р - выросли цены
18 000 + 3 600 = 21 600 р - цена в июне и новые 100%
21 600 : 100 = 216р - новый 1%
Цена в июле- 15 300
21 600 - 15 300 = 6 300 - сумма, на которую понизили цену
6300 : 216 = 29,17% примерно
6300 : 180 = 35%
Если моё решение оказалось верным, я бы хотел Вас попросить отметить мой ответ как лучший, а так же оставить отзыв о качестве моей работы (каким бы он ни был). Рад был оказать Вам
Проведем ОК⊥AB, OL⊥BC, OM⊥CD и ON⊥AD.
Проведенные отрезки - проекции соответствующих наклонных на плоскость ромба, значит и наклонные перпендикулярны сторонам ромба по теореме о трех перпендикулярах.
Т.е. FK = FL = FM = FN = 16 см - расстояния от точки F до сторон ромба.
Если равны наклонные, проведенные из одной точки, то равны и их проекции:
OK = OL = OM = ON, значит О - центр окружности, вписанной в ромб, т.е. точка пересечения его диагоналей.
ΔAOD: ∠AOD = 90°, AO = 8 см, DO = 6 см по свойству диагоналей ромба.
По теореме Пифагора AD = √(AO² + DO²) = √(64 + 36) = 10 см
ON = AO·DO / AD = 6·8 / 10 = 4,8 см
ΔFON: ∠FON = 90°, по теореме Пифагора
FO = √(FN² - ON²) = √(256 - 576/25) = √(5824/25)
ΔFOD: по теореме Пифагора
FD = √(OD² + FO²) = √(36 + 5824/25) = √(6724/25) = 82/5 = 16,4 см
ΔAOF: по теореме Пифагора
FA = √(AO² + FO²) = √(64 + 5824/25) = √(7424/25) = 16√29/5 см
FB = FD = 16,4 см
FA = FC = 16√29 / 5 см так как треугольники FBD и FAC равнобедренные (FO в них высота и медиана)