ответ: 8√3 см²
Пошаговое объяснение:
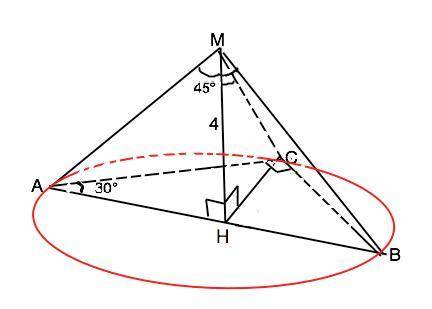
Обозначим пирамиду МАВС. Высота МН пирамиды перпендикулярна основанию и образует с боковыми ребрами углы 45°, следовательно, второй острый угол тоже 45°, боковые ребра - гипотенузы равных прямоугольных равнобедренных треугольников с общим катетом - высотой пирамиды, а их проекции равны радиусу описанной около основания окружности. Вершина пирамиды проецируется в центр этой окружности, – середину гипотенузы основания. АН=СН=ВН=МН=4 см, АВ=2•4=8 см. Катет АС=АВ•cos∠CAB=8•√3/2=4√3. Одна из формул площади треугольника S=0,5•a•b•sinα. ⇒ S(ABC)=0,5•0,AB•AC•sin30°=0,5•8•4√3•1/2=8√3 см²
ответ: 8√3 см²
Пошаговое объяснение:
Обозначим пирамиду МАВС. Высота МН пирамиды перпендикулярна основанию и образует с боковыми ребрами углы 45°, следовательно, второй острый угол тоже 45°, боковые ребра - гипотенузы равных прямоугольных равнобедренных треугольников с общим катетом - высотой пирамиды, а их проекции равны радиусу описанной около основания окружности. Вершина пирамиды проецируется в центр этой окружности, – середину гипотенузы основания. АН=СН=ВН=МН=4 см, АВ=2•4=8 см. Катет АС=АВ•cos∠CAB=8•√3/2=4√3. Одна из формул площади треугольника S=0,5•a•b•sinα. ⇒ S(ABC)=0,5•0,AB•AC•sin30°=0,5•8•4√3•1/2=8√3 см²

S(¥x+1)/x^2 dx= $¥x/x^2 dx + $1/x^2 dx=$(x)^(-3/2)dx+$(x)^(-2)dx= -2x^(-1/2) - x^(-1) + C= -2/¥x -1/x + C.
C-постоянная.
¥-корень.