Заметим, что если у нас в какой-то момент времени на прямой оказалось  точек, то после "удвоения" точек станет ровно
точек, то после "удвоения" точек станет ровно 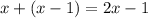 .
.
То есть, чтобы узнать, сколько точек было до 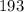 точек, нужно решить уравнение
точек, нужно решить уравнение 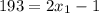 . Понятно, что
. Понятно, что 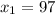 .
.
Узнаем, сколько точек было до 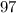 :
: 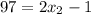 . Здесь
. Здесь 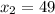 .
.
Очередным уравнением будет 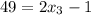 и
и 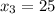 .
.
Далее 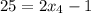 , откуда
, откуда 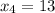 .
.
По аналогии 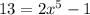 , и, конечно
, и, конечно 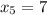 .
.
И, заключительный шаг, 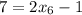 , где
, где 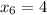 .
.
А уравнение 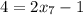 имеет ненатуральный корень
имеет ненатуральный корень  , точек на количество прямой не может быть дробным числом.
, точек на количество прямой не может быть дробным числом.
Получаем, что максимальное значение 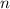 равно
равно 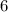 :
:
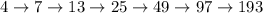
То есть, больше 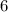 шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
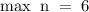
Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 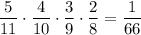 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна  . По теореме умножения
. По теореме умножения 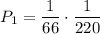
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 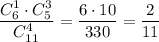 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 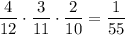 . По теореме умножения:
. По теореме умножения: 
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 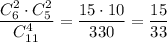 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 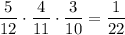 . По теореме умножения :
. По теореме умножения : 
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна  . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна  . По теореме умножения:
. По теореме умножения: 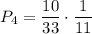
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 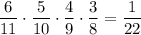 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 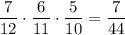 . По теореме умножения:
. По теореме умножения: 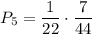
Итого, по теореме сложения:

136-128=8 пл.
1м=100см
12м=1200см
1200:8=150 см-на 1 пл
136*150=20400см =204 м-на 136 пл
128*150=19200см=192м -на 128 пл.