Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
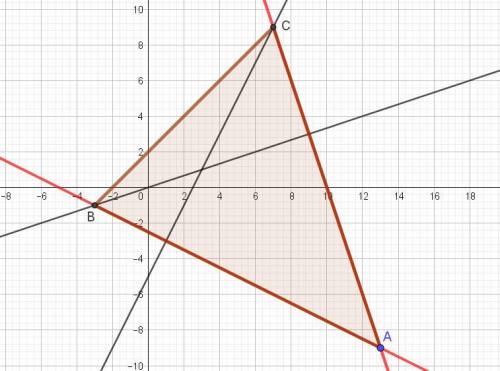
В решении.
Пошаговое объяснение:
5. Задача:
Расстояние между двумя пристанями теплоход проходит по течению реки за 1,5 часа, а против течения за 2 часа. Собственная скорость теплохода а км/ч, а скорость течения реки b км/ч. Составьте выражение по условию задачи для нахождения расстояния:
Формула движения: S=v*t
S - расстояние v - скорость t – время
(a + b) - скорость теплохода по течению.
(a + b) * 1,5 - расстояние теплохода по течению.
(a - b) - скорость теплохода против течения.
(a - b) * 2 - расстояние теплохода против течения.
Расстояние между пристанями одинаковое.
По условию задачи уравнение:
(a + b) * 1,5 = (a - b) * 2
2)1000 : 4 = 250
3)250 : 50 = 5