1) Дать определение: число a больше числа b
a > b, ели a − b > 0
Число a больше числа b, если разность этих чисел положительна.
2) Сравнить:
а)
8/11 и 9/13
Вычтем из первого числа второе:
 и 0
и 0
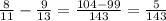
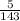 и 0
и 0
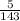 > 0
> 0
Значит, 
б)
a²+16 и 8a
Вычтем из первого выражения второе:
a²−8a+16 и 0
(a−4)² и 0
по определению, вырежение в квадрате всегда дает число неотрицательное, то есть (a−4)²≥0
(a−4)² = 0, если a = 4
(a−4)² > 0, если a ≠ 4
Значит, a² + 16 > 8a, если a ≠ 4; и a²+16 = 8a, если a = 4.
3) Доказать неравенство:
(a−3)(a+11) < (a+3)(a+5)
a²+11a−3a−33 < a²+5a+3a+15
Вычтем из первого выражения второе:
a²+11a−3a−33−a²−5a−3a−15 и 0
−48 и 0
Значит, (a−3)(a+11) < (a+3)(a+5), что и требовалось доказать.
4) Сравнить числа а и b, если верно неравенство: 3a−3b ≥ 1
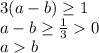
5) Оценить величину: 5а−2, если 1,1 < а ≤ 1,2
Умножим все части неравенства на 5:
5·1,1 < 5a ≤ 5·1,2
5,5 < 5а ≤ 6
Вычтем из всех частей неравенства 2:
5,5−2 < 5а−2 ≤ 6−2
Получаем:
3,5 < 5а−2 ≤ 4
при n = 2, p = 47 при n = 22, p = 547
при n = 3, p = 53 при n = 23, p = 593
при n = 4, p = 61 при n = 24, p = 641
при n = 5, p = 71 при n = 25, p = 691
при n = 6, p = 83 при n = 26, p = 743
при n = 7, p = 97 при n = 27, p = 797
при n = 8, p = 113 при n = 28, p = 853
при n = 9. p = 131 при n = 29, p = 911
при n = 10, p = 151 при n = 30, p = 971
при n = 11, p = 173 при n = 31, p = 1033
при n = 12, p = 197 при n = 32, p = 1097
при n = 13, p = 223 при n = 33, p = 1163
при n = 14, p = 251 при n = 34, p = 1231
при n = 15, p = 281 при n = 35, p = 1301
при n = 16, p = 313 при n = 36, p = 1373
при n = 17, p = 347 при n = 37, p = 1447
при n = 18, p = 383 при n = 38, p = 1523
при n = 19, p = 421 при n = 39, p = 1601
при n = 20, p = 461 при n = 40, p = 1681 = 41 * 41. (а это уже составное)