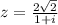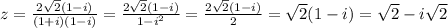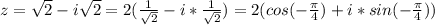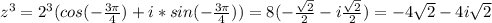Для первого : 1. найдите область определения функции и область значений функции. 2. найдите производную - id864631220220803 от andrewbukharin2 03.08.2022 12:13

Question

Математика: Для первого : 1. найдите область определения функции и область значений функции. 2. найдите производную данной функции, определите точки экстремума, интервалы возрастания и убывания. 3. постройте график функции, отметьте на нем точки экстремума. для второго - вычислить заданные пределы

andrewbukharin2 · Accepted Answer

1) Произвольное комплексное число z в алгебраической форме: z = a + b*i Оно же в тригонометрической форме: z = r*(cos Ф + i*sin Ф) Здесь r = √(a^2 + b^2); Ф = arctg(b/a) 2) z = 1 - i a = 1; b = -1; r = √(1^2 + (-1)^2) = √2; Ф = arctg(-1/1) = -pi/4 z = √2*(cos(-pi/4) + i*sin(-pi/4)) 3) Сначала представим z в обычном алгебраическом виде: Для этого умножим числитель и знаменатель на комплексно-сопряженное. Теперь переведем его в тригонометрическую форму Здесь нам номер 2), в котором мы уже представляли...

MOGZ ответил