1.1) Сумма пяти нечетных чисел и пяти четных нечетна, поэтому число 8 не получится.
1.2)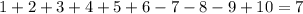 
2) Пусть длина отрезка x см. Тогда в первом измерении получили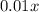 
метров, а во втором - 
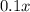дециметров, на 81 больше, чем 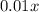. Составляем уравнение:
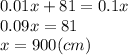
ответ: 900 см.
3) После каждого друга оставалось по 2/3 от количества орехов. Тогда до его просыпания орехов было в 1.5 раза больше, чем после того, как он съел свою треть (он съедает 0.5 остатка). Тогда третий съел 8 орехов, а до него было 24 ореха; второй съел 12 орехов, до него было 36 орехов ; первый съел 18 орехов, а до него было 54 ореха. Каждому должно было достаться по 18 орехов, поэтому распределяем оставшиеся орехи так: второму - 4 ореха, а третьему - 10 орехов.
Докажите, что 11 коней не
могут побить все оставшиеся поля шахматной доски.
Решение. Закрасим на доске 12 полей
(см. рисунок). Никакие два из этих полей не могут быть побиты одним конем.
Значит, чтобы побить даже только раскрашенные поля, понадобится минимум
12 коней
Пошаговое объяснение:
Комментарий к решению. Идея выделить 12 полей так,
чтобы никакие два не бились одним конем— достаточно типовая. Заметив, что 12 кратно 4, естественно попытаться
использовать симметрию доски. Тройки закрашенных полей естественно пытаться рассовывать по углам подальше
друг от друга.
Информацию о числе (а еще лучше — о расположении) узких мест
можно и нужно использовать и при построении примера. В частности,
этот прием встречается в задачах типа «Оценка
+ пример».
тд, возможно глупо, но...