a)lim x->oo (x^2+3x-4)/x^5=lim x->oo (1/x^3+3/x^4-4/x^5)/1 -- мы разделили числитель и знаменатель на x со старшей(с самой большой) степенью. В данном случае на x^5. Теперь мысленно подставим оо под х и получим: 0+0-0=0(1/x^3=3/x^4=4/x^5=0, так как с увеличением х число уменьшается. А значит, стремится к нулю.)
ответ: 0.
Аналогично выполним всё первое задание:
б)lim x->oo (x^5+2x-3)/(4x^3-8)=lim x->oo (1+2/x^4-3/x^5)/(4/x^2-8/x^5) -- и снова делим на старшую(на пятую в данном случае) степень. Далее всё по аналогии: (1+0-0)/(0-0)=1/0=оо(0 под очень маленьким числом подразумевается. И чем меньше оно, тем больше ответ будет, поэтому оо.)
ответ: оо.
Далее всё то же самое; нет смысла объяснять.
в)lim n->oo (3-4n+2n^5)/(2n^2+n-n^4)=lim n->oo (3/n^5-4/n^4+2)/(2/n^5+1/n^4-1/n)=(0-0+2)/(0+0-0)=2/0=oo.
ответ: оо.
г)lim n->oo (n^3+20n-4)/(16n+13)=lim n->oo (1+20/n^2-4/n^3)/(16/n^2+13/n^3)=(1+0-0)/(0+0)=1/0=oo.
ответ: оо.
Пошаговое объяснение:
Задание 1
Мы приходим к общему знаменателю с метода "бабочка" : Суть «метода бабочки» заключается в том, чтобы прийти к общему знаменателю дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой , и знаменатель второй на знаменатель первой .
Задание 2
Смысл тот же , только теперь сложение . Используем метод бабочки и складываем ( Суть «метода бабочки» заключается в том, что при сложении дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой. Сумма двух получившихся чисел будет числителем дроби в ответе, а ее знаменателем — результат умножения знаменателей складываемых дробей).
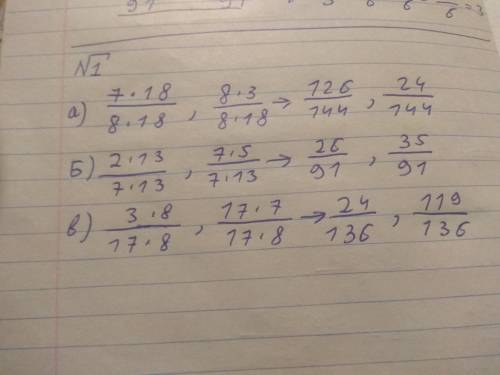
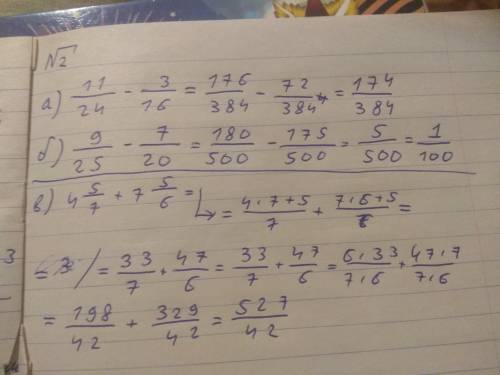
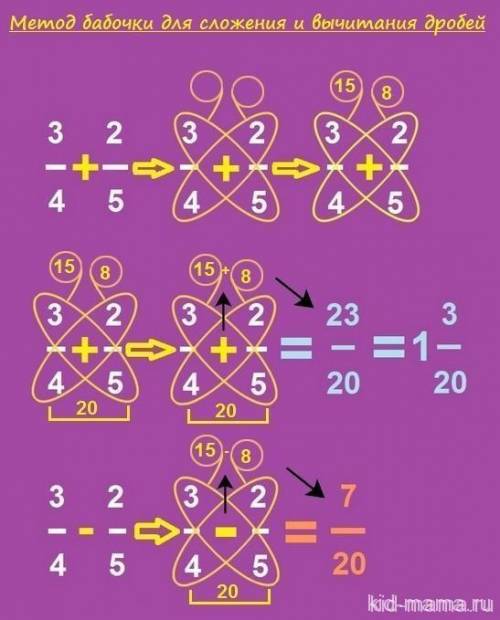
8см в кв=64см.
3м в кв =9м=900см
1)900+250+64=1214см.
ответ:1214 см.