Возьмём производную. Если производная в данной точке больше 0, функция растёт и наоборот.
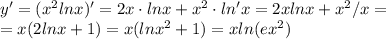
Если подлогарифмическое выражение больше 1, то логарифм больше единицы.
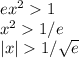
Если логарифм больше 0, то при отрицательных х производная меньше 0 (x<-1/sqrt(e)), при положительных - больше 0 (x>1/sqrt(e)).
Если логарифм меньше 0 (|x|<1/sqrt(e)), то при положительных х производная меньше 0 (0<x<1/sqrt(e)), при отрицательных - больше 0 (-1/sqrt(e)<x<0)
В крайних точках функция определена (кроме х=0), значит интервалы включают крайние значения.
Функция убывает при ![x\epsilon(-\infty;-1/\sqrt{e}]\cup(0;1/\sqrt{e}]](/tpl/images/0150/0553/0bd51.png)
Возрастает при 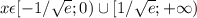
От начального количества зависит не столько стратегия, сколько тот, кто выиграет, начиная первым, если оба будут играть наилучшим для себя образом.
Стратегия - надо оставлять противнику количество лепестков, кратное 3 (т.е. 3, 6, 9 и т.п.), тогда он сможет оборвать один или два, а вы следующим ходом дополняете обрыв опять до кратного 3 (т.е. вы оставили ему, например, 9 лепестков, он оборвал 1 - вы обрываете 2 - оставляя ему 6 и т.д.) - тогда, увидев только 3 лепестка он вынужден будет оборвать только 1 или 2 - а вы оборвете оставшиеся.
Поэтому, если число лепестков изначально кратно 3, то начинающий - проигрывает, в других случаях - выигрывает.