Пошаговое объяснение:
тут может быть ошибка в записи - либо у=х² -12-5, либо у=х² -12х-5
я рассмотрела оба варианта, как по теории положено делать
ОДНАКО
ПРИМЕЧАНИЕ
график и той и другой функций - парабола ветвями вверх. точки максимума могут быть рассчитаны только на отрезках. на всей ООФ такие функции не имеют точек максимума
1) если у = х² - 12 + 7
точки экстремума
у(x) = 0 - это необходимое условие экстремума функции
y' = 2x; 2х=0 ⇒ х=0; х₀=0 - это точка экстремума
посмотрим - это минимум или максимум
по теории
если у''(х₀) > 0 то х₀ - точка минимума функции.
если у'(х₀) < 0 , то х₀ - точка максимума.
у нас
y'' = 2
y''(0) = 2>0 - значит точка х₀ = 0 точка минимума функции.
у нашей функции максимума нет
2) если у = х² - 12х + 7
то будет такое решение (теорию уже писать не буду)
найдем точки экстремума
y' = 2x-12
2x-12 = 0 ⇒ 2(x-6) =0 ⇒ x = 6
y'' = 2
y''(6) = 2>0 - значит точка х₀ = 0 точка минимума функции.
и у этой функции максимума нет
Пункт 5) -26 .
Пошаговое объяснение:
Раскроем знак модуля:
1)Если х>0 ⇒ |x|=х ⇒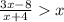 
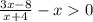
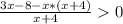
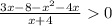
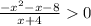
Так как числитель -x²-x-8<0 ,
а знаменатель x+4>0 ⇒
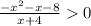неравенство
невыполнимо : ∅
2)Если x<0 ⇒ |x|=-x ⇒
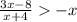
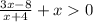
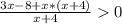
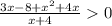
3x-8+x²+4x=0
x²+7x-8=0
D=49-4·(-8)=81=9²>0
x₁=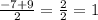
x₁=1>0 выпадает, так как положительно,
что противоречит выбранному условию.
x₂=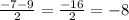
x₂=-8<0 подходит.
++++++++ _ _ _ _ _ _ _ _ _ _ _ ++++++++++++
--------------|-------------------------------|----------------------
_ _ _ _ _ -8_ _ _ _ _ +++++++1++++++++++++++
----------------------------|----------------------------------------
-4
x∈[-8; -4)∪[1: +∞)
Целые решения неравенства :
-8; -7; -6; -5.
Сумма всех целых решений
неравенства:
-8-7-6-5= -26 .
2)640/20=32см длина доски
32>30 значит можно