![\max f(x \in[0;\;\pi] ) = f(0) = \frac{4}{3} \\ \min f(x \in[0;\;\pi] ) = f(\pi) = - \frac{4}{3}](/tpl/images/1875/1181/9b301.png)
Пошаговое объяснение:
![f(x) = \cos{x} + \frac{1}{3} \cos(3x) \\ \max f(x \in[0;\;\pi] )](/tpl/images/1875/1181/415f2.png)
Функция непрерывна и определена на R, а следовательно и на всем заданном отрезке.
Максимальное значение f(x) на отрезке может быть:
- на концах заданного отрезка
- в точках экстремума функции.
Т.е. следует проверить значения функции в точках
1) где f'(x)=0
2) х = 0; х = П
1) Найдем производную f'(x)
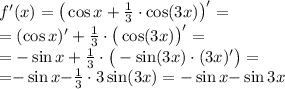
Найдем нули производной:
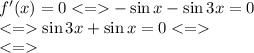
Применим формулу
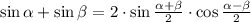
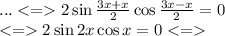
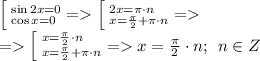
При
![x \in[0;\;\pi] \\0 \leqslant x = \frac{\pi}{2} \cdot{n} \leqslant \pi \\ 0 \leqslant \frac{n}{2} \leqslant 1 \\ 0 \leqslant {n} \leqslant 2 = n \in \: \{0;\;1;\;2 \} \\ x = \{0;\; \frac{\pi}{2} ;\;\pi\}](/tpl/images/1875/1181/f47fd.png)
Проверим точки: (кстати, концы отрезка также входят в точки экстремума функции)
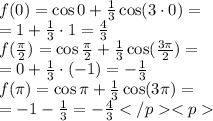
Мы видим, что максимальное и минимальное значение функции достигается в точках:
Відповідь:
1) 21.134
2) 371000
3) 6692
4) 42292
5) 10,68
Покрокове пояснення:
1) 16728 : 82 − 5580 : 45 + 726 • 29 Виконуємо поділ. Обчислювати
204-124+21054 Обчислювати
21.134
2) (39 002 − 37 236) • 205 + 115 • 78 Обчислювати
1766*205+8970 Обчислювати
362030+8970 Обчислювати
371000
3) 875 • 480 − 406 • (50 004 − 48 986) Обчислювати
420000-406*1018 Обчислювати
420000-413308 Обчислювати
6692
4) (53734 : 67 − 59 925 : 85) • 436 Виконуємо поділ
(802-705)*436 Обчислювати
97*436 Обчислювати
42292
5) 61 − (1428 : 136 + 4,3) • 3,4 Виконуємо поділ
61-(10,5+4,3)*3,4 Обчислювати
61-14,8*3,4 Обчислювати
61-50,32 Обчислювати
10,68
2 действие: 240:80=3(кг)
ответ: 3 кг муки положили в каждый пакет