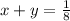 - бассейнов в час наполняют 1-я и 2-я трубы вместе,
- бассейнов в час наполняют 1-я и 2-я трубы вместе,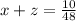 - бассейнов в час наполняют 1-я и 3-я трубы вместе,
- бассейнов в час наполняют 1-я и 3-я трубы вместе,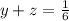 - бассейнов в час наполняют 2-я и 3-я трубы вместе;
- бассейнов в час наполняют 2-я и 3-я трубы вместе;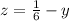
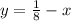
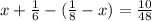
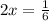
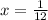 - бассейнов в час наполняет 1-я труба;
- бассейнов в час наполняет 1-я труба;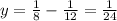 - бассейнов в час наполняет 2-я труба;
- бассейнов в час наполняет 2-я труба;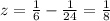 - бассейнов в час наполняет 3-я труба;
- бассейнов в час наполняет 3-я труба;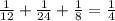 бассейнов в час наполняют три трубы вместе;
бассейнов в час наполняют три трубы вместе;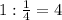 (часа) - наполняют 1 бассейн три трубы вместе
(часа) - наполняют 1 бассейн три трубы вместе
675 кг-?
1) 675:20=33 (кг)-останется
2) 33*20=660 (кг)-разложат в 33 ящика по 20 кг
3) 675-660=15 (кг)-моркови будет в последнем ящике
3) 33+1=34 (ящ)-потребуется, чтобы отправить в магазин 675 кг