Если точка К равно удалена от всех вершин трапеции, то эта трапеция вписана в окружность радиуса R.
Из условий, что боковая сторона перпендикулярна диагонали и трапеция вписана в окружность, следует, что большее основание трапеции - равно 2R, то есть диаметру описанной окружности.
В прямоугольном треугольнике произведение катетов равно произведению гипотенузы на высоту h из прямого угла.
Пусть боковая сторона трапеции равна х, диагональ - d.
Тогда xd = 2Rh, или 40х = 2R*24. Отсюда х = 48R/40 = 6R/5.
С другой стороны, по Пифагору, (2R)² = x² + d² = (36R²/25) + 40².
4R² - (36R²/25) = 1600.
64R²/25 = 1600.
Отсюда определяем значение R = √(1600*25/64) = 40*5/8 = 25 см.
Теперь можно найти расстояние Н от точки К до плоскости трапеции:
Н = √(65² - R²) = √(4225 - 625) = √3600 = 60 см.
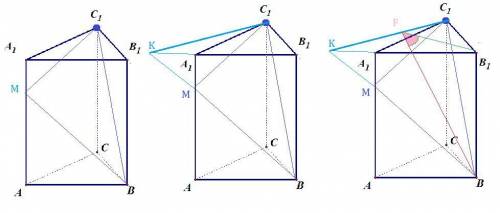
Плоскость АВС || плоскости A₁B₁C₁
Поэтому удобнее искать угол между ВМС₁ и A₁B₁C₁
Надо найти линию пересечения этих плоскостей.
Одна общая точка - точка С₁.
Прямые А₁В₁ и ВМ лежат в пл. АА₁В₁В
Найдем их точку пересечения. Это точка К
Значит пл. ВМС₁ и пл. A₁B₁C₁ пересекаются по прямой С₁К
Осталось провести к этой прямой перпендикуляры. B₁F в пл. A₁B₁C₁
BF в пл. ВМС₁
tg∠B₁FB=BB₁/B₁F
Из подобия А₁КМ и В₁КВ
KA₁:KB₁=A₁M:B₁B
KA₁=4/3
Из треугольника КВ₁С₁ по теореме косинусов
KC₁²=((4/3)+4)^2+4^2-2·(4/3)+4)·4cos∠A₁B₁C₁=(16/3)^2+16-2·(16/3)·4·
1/2=(256/9)+(144/9)-(64/3)=(400-64*3)/9=208/9
KC₁=4√(13)/3
tg∠B₁FB=BB₁/B₁F=8:(4(13)/3)=(6√13)/13
О т в е т. ∠B₁FB= arctg(6√13)/13