Объём призмы равен произведению ее высоты на площадь основания.
Т.к. призма прямая, ее ребра перпендикулярны основанию и высота призмы равна длине бокового ребра.
В основании квадрат большей стороны треугольника больше суммы квадратов двух других сторон, следовательно, ∆ АВС - тупоугольный, и высота ВН, проведенная к меньшей стороне, - вне треугольника.
Сделаем рисунок. Проведем высоту основания к меньшей стороне, выразим ее квадрат из прямоугольных треугольников СВН и АВН и приравняем выражения.
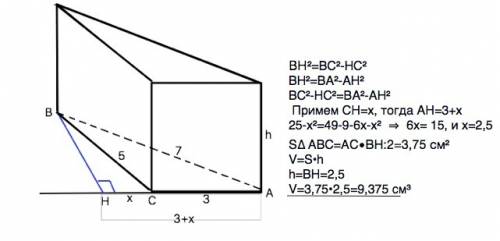
ВН²=ВС²-НС²
ВН²=ВА²-АН²
ВС²-НС²=ВА²-АН²
Примем СН=х, тогда АН=3+х
25-х²=49-9-6х-х² ⇒ 6х= 15, и х=2,5
S∆ АВС=AC•BH:2=3,75 см²
V=S•h
h=BH=2,5
V=3,75•2,5=9,375 см³
x^2-2x+3-2/x+1/x^2=0
(x^2+1/x^2)-2(x+1/x)+3=0
t=x+1/x
t^2-2-2t+3=0
t^2-2t+1=0
(t-1)^2=0
t-1=0
t=1
x+1/x=1
x^2-x+1=0
D=-3<0
x - нету корней
ответ: нету корней