1 (-бесконечность;+бесконечность) 2 (- бесконечность;-7\4)U(-7\4;+бесконечность) 3 [-7;+бесконечность) 4 (-бесконечность;1/2) 5(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность) 6(-бесконечность;+бесконечность)
Пошаговое объяснение:
Область определения это такие числа, которые может принимать переменная x.
1. 
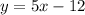(здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)
2. 
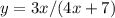(В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)
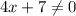
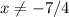=> (- бесконечность;-7\4)U(-7\4;+бесконечность)
3.
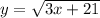(Под корнем всегда должно быть неотрицательное число)
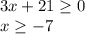[-7;+бесконечность)
4.
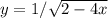(знаменатель не должен быть равен 0, а так же не должен быть отрицательным)
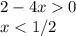(-бесконечность;1/2)
5. 
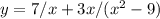(знаменатель не должен быть равен 0)
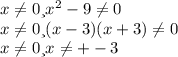(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность)
6.
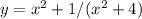(знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)
(-бесконечность;+бесконечность)
Степень многочлена - это наибольшая степень входящего в него одгночлена.
Степень одночлена - это сумма степеней всех переменных, входящих в его состав.
а) многочлен 3х⁵ + 2х³ + 4 состоит из следующих членов: 3х⁵; 2х³ и 4, его степень - 5;
б) многочлен 2х⁴ - 3х + 2 состоит из следующих членов: 2х4; -3х и 2, его степень - 4;
в) многочлен х⁵ + х⁴ - 2х² - 1 состоит из следующих членов: х⁵; х⁴; -2х² и -1, его степень - 5;
г) многочлен 2m⁶ + 7 состоит из следующих членов: 2m⁶ и 7, его степень - 6;
д) многочлен 4ху⁶ + ху² - х² + у⁸ состоит из следующих членов: 4ху⁶; ху²; -х² и у⁸, его степень - 8;
е) многочлен а³ - bc - 7 состоит из следующих членов: a³; -bc и -7, его степень - 3.
где {\displaystyle x} — неизвестное, {\displaystyle a}, {\displaystyle b}, {\displaystyle c} — коэффициенты, причём {\displaystyle \quad a\neq 0.}
Выражение {\displaystyle ax^{2}+bx+c} называют квадратным трёхчленом[1].
Корень — это значение переменной {\displaystyle x}, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.
Элементы квадратного уравнения имеют собственные названия[1]:
{\displaystyle a} называют первым или старшимкоэффициентом,{\displaystyle b} называют вторым, средним или коэффициентом при {\displaystyle x},{\displaystyle c} называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент {\displaystyle a}:
{\displaystyle x^{2}+px+q=0,\quad p={\frac {b}{a}},\quad q={\frac {c}{a}}.}
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.