Пошаговое объяснение:
а) у = -1/3 х
А(6;-2) -1/3 * 6 = -2; -2 = -2 точка принадлежит данному гр функции
В(-2; -10) -1/3 * (-2) = 2/3; 2/3 ≠-10 точка не принадлежит
С(1; - 1) -1/3 * 1 = -1/3 ; - 1/3 ≠-1 точка не принадлежит гр функции
Д(-1/3; 1_2/3) -1/3 * (-1/3) = 1/9; 1/9 ≠1_2/3 точка не принадлежит
Е(0; 0) -1/3 * 0 = 0 ; 0 = 0 точка принадлежит гр функции
Точку (0; 0) можно было и не проверять, так как в условии сказано, что это график прямой пропорциональности, а её график всегда проходит через начало координат - точку (0; 0)
б) у = 5х
А(6; -2) 5*6 = 30; 30≠-2 не принадлежит гр функции
В(-2; -10) 5 * (-2) = -10; -10 = -10 точка принадлежит гр функции
С(1; -1) 5 * 1 = 5; 5≠-1 точка не принадлежит гр функции
Д(-1/3; 1_2/3) 5 * (-1/3) = - 5/3; - 5/3 ≠ 5/3 точка не принадлежит гр функции
Е(0;0) принадлежит гр функции
Пошаговое объяснение:
1. Точный расчет по формуле Ньютона-Лейбница.
Интеграл - площадь под графиком функции вычисляем по формуле:
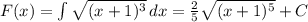
Вычисляем на границах интегрирования.
F(3) = 64/5, F(1) = 8/5*√2.
И сам определенный интеграл:
F = F(3) - F(1) = (64-8√2)/5 = 10.5373 - точное значение - ответ.
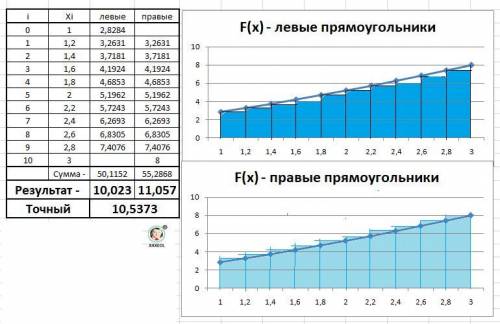
2. Приближенное вычисление по формулам прямоугольников.
Площадь фигуры разбивается на прямоугольники ширина которых зависит от числа точек расчёта - h = (b-a)/n, а высота равна значению функции.
Если за высоту брать значение с левой стороны отрезка получим формулу левых прямоугольников:
Fлев ≈ (b -a)/n*[f(x₀)+f(x₁)+...+f(xₙ-₁)] - и результат будет меньше точного значения.
Fправ ≈ (b -a)/n*[f(x₁)+f(x₂)+...+f(xₙ)] - больше точного значения.
Расчет и схема расчета приведена в приложении.
Для n = 10, получаем значение h = (3-1)/10 = 0.2.
Получили два значения интеграла:
Fлев = 10,023 и Fправ = 11,057.
Абсолютную погрешность вычисления находим по формуле:
Δ = (Fлев - F) = 10.023 - 10.5373 = - 0.514 и
Δ = (Fправ - F) = 11.057 - 10.5373 = 0.520
Абсолютная погрешность Δ = ± 0,52 - ответ.
Относительная погрешность вычисляется в процентах:
δ = Δ/F = 0,52 : 10,5373 = 0.05 = 5% - относительная погрешность - ответ.
Тогда вероятность события A={стрелок попал двумя выстрелами} равна: