В решении.
Пошаговое объяснение:
Представьте бесконечную десятичную периодическую дробь 7,1(6) в виде обыкновенной.
Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно из числа, стоящего после запятой до второго периода, вычесть число, стоящее после запятой до первого периода, и эту разность сделать числителем, а в знаменатель записать цифру 9 столько раз, сколько цифр в периоде, со столькими нулями справа, сколько цифр между запятой и первым периодом.
7,1(6) = 7 ((16-1)/90) = 7 15/90.
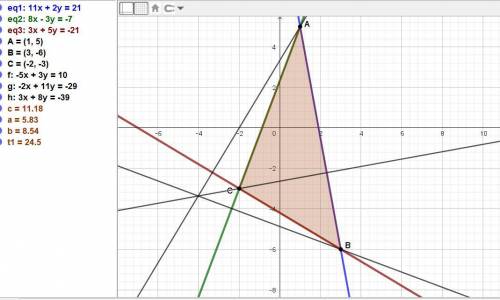
Даны уравнениям сторон треугольника:
11x+2y-21=0
8x-3y+7=0
3x+5y+21=0.
В уравнении перпендикулярной прямой коэффициенты А и В в уравнении вида Ах + Ву + С = 0 меняются на -В и А.
Возьмём первую сторону (пусть это АВ, получаем уравнение высоты из точки С: -2х + 11у + С = 0. Чтобы определить слагаемое С уравнения надо подставить координаты точки, через которую проходит прямая.
Находим вершины треугольника, решая системы из двух уравнений сторон. Точка А:
{11x+2y-21=0 |x(3) = 33x + 6y - 63 = 0
{8x-3y+7=0 |x(2) = 16x - 6y + 14 = 0
49x - 49 = 0, х = 49/49 = 1.
у = (21 - 11х)/2 = (21 - 11*1)/2 = 10/2 = 5. Точка А(1; 5).
Аналогично определяем точки: В(3; -6) и С(-2; -3).
Теперь находим С в уравнении высоты из точки С.
-2*(-2) + 11*(-3) + С = 0,
С = 33 - 4 = 29. Уравнение -2х + 11у + 29 = 0.
Аналогично находим уравнения высот из точек А и В.
Высота из точки А: -5х + 3у - 10 = 0,
из точки В: 3х + 8у + 39 = 0.
3=5sin<A
sin<A=3/5
BA=ACcos<A
4=5cos<A
cos<A=4/5
CB=ABtg<A
3=4tg<A
tg<A=3/4
2)BC=ACsin<A
12=13sin<A
<A=12/13
AB^2=AC^2-BC^2=169-144=25; AB=5
AB=CBtg<C
5=12tg<C
tg<C=5/12
3)BC=ACcos<C=15*0,6=9
4)Другой острый угол равен 180-(90+60)=30 град
Катет противолежащий углу 30 град равен 1/2 гипотенузы, значит катет равен 8/2=4см. Тогда по теореме Пифагора второй катет равен
sqrt 64-16=sqrt 48=4 sqrt 3см
5)Высота BD делит треугольник АВС на два прямоугольных треугольника. Рассмотрим треугольник ABD. BD=ABsin<A; h=ABsina; AB=h/sina. Так как треугольник равнобедренный,то АВ=ВС=h/sina
6)Обозначим ромб как АВСД. Тогда угол АВС=60 град. ВД=10. Проведем вторую диагональ АС. Пусть диагонали ромба пересекаются в точке О. Диагонали являются биссектрисами его углов,тогда угол АВО=углу ОВС=30град. При пересечении диагонали точкой пересечения делятся по палам т.е. ВО=ОД=5. Рассмотрим треугольник АВО-прямоугольный,т.к. диагонали ромба пересекаются под прямым углом.Найдем сторону ромба: ВО=АВсos<OAB; 5=АВ cos30; 5=АВ sqrt3/2; АВ=10/sqrt3. АО= 5tg<ABO; AO=5tg30; AO=5*sqrt3/3, тогда диагональ равна 2АО=АС=10sqrt3/3
7) Так как трапеция равнобедренная,то углы у нее при основаниях равны, <A=<D=a. Треугольник ACD-прямоугольный. Тогда CD=ADcos<D;
CD=bcosa. опусти из вершины тупого угла С высоту на основание трапеции AD и обозначим ее СН. Треугольник CHD-прямоугольный. Найдем СН. СН= CDsin<D=bcosasina. Теперь найдем HD. HD=CDcos<D=
=bcos^2a. Из вершины В опусти так же высоту и обозначим ВН1. так трапеция равнобедренная,то АН1=HD=bcos^2a. Тогда BC=AD-2AH1=
=b-2bcos^2a
P= AB+BC+CD+AD=2bcosa+b-2bcos^2a+b=2bcos^2a+2bcosa+2b :(2b)
cos^2a+cosa+1
S=AB+BC/2*CH=2b-2bcos^2a/2*bcos^2a=(1-cos^2a)b^2cos^2a