Математика: Y=x^4-2x^2 дослідження функції на монотоність за похідної

Y=x^4-2x^2 дослідження функції на монотоність за похідної

👇

Увидеть ответ

Ответ:

Артём89535014367

13.04.2022

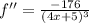ДАНО

Y = x⁴ - 2*x²

ИССЛЕДОВАНИЕ

1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.

Вертикальной асимптоты нет.

2. Пересечение с осью Х. Y=x²*(x-√2)*(x+√2).

Корни:х₁ = 0, х₂ = -√2, х₃ = √2

Интервалы знакопостоянства:

Положительная - X∈(-∞;-√2)∪(√3;+), отрицательная - X∈(-√2;√2).

3. Пересечение с осью У. У(0) = 0.

4. Поведение на бесконечности. limY(-∞) = +∞ limY(+∞) = +∞

Горизонтальной асимптоты нет.

5. Исследование на чётность.Y(-x) = Y(x).

Функция чётная.

6. Производная функции.Y'(x)= 4*x³ -4x = x*(x-1)*(х+1) = 0.

Корни: x₁= 0, x₂ = - 1, x₃ = 1

7. Локальные экстремумы.

Максимум Ymax(0)= 0, минимум – Ymin(-1)= Y(min(1) = -1.

8. Интервалы монотонности.

Возрастает - Х∈[-1;0]∪[1;+∞), убывает = Х∈(-∞;-1]∪[0;1].

8. Вторая производная - Y"(x) =12*x² -4=0. x= +/-√(1/3)

Корни производной - точки перегиба - х₁ =-√3/3, х₂ = √3/3 ≈ 0.58.

9. Выпуклая “горка» Х∈[-√3/3; √3/3],

Вогнутая – «ложка» Х∈(-∞;-√3/3]∪[√3/3;+∞).

10. Наклонной асимптоты - .

lim(+∞)Y(x)/x = x³ - 2*x = +∞ - нет

10. График в приложении.
Y=x^4-2x^2 дослідження функції на монотоність за похідної

4,4(92 оценок)

Открыть все ответы

Ответ:

veronikamihailova37

13.04.2022

Найдем производную, приравняем ее к нулю. найдем критические точки, разобьем область определения функции на промежутки и установим знак на каждом из них. где производная больше нуля - там функция возрастает, где она меньше нуля. функция убывает. при переходе через критическую точку : если производная меняет знак с плюса на минус, то это точка максимума, с минуса на плюс - точка миниимума, а значения функции в этих точках - соответственно максимум и минимум.

f'(x)=(x³/3+x²-3x-1)'=x²+2x-3

x²+2x-3=0 По Виету х=-3, х=1, неравенство решим методом интервалов (х+3)(х-1)<0

-31

+ - +

На промежутках (-∞;-3] и [1;+∞) функция возрастает, а на

[-3;1] убывает. Точка х= -3 - точка максимума, а х=1- точка минимума, максимум равен -27/3+9+9-1=8; минимум равен

1/3+1²-3-1-2 2/3

4,6(81 оценок)

Ответ:

drazzgaming

13.04.2022

1) Находим область определения: вся числовая ось, кроме х = -5 / 4 (при этом значении знаменатель превращается в ноль).
2) Находим точки пересечения с осями:
х = 0 у = -3/5 это точка пересечения с осью у.
у = 0 надо числитель приравнять 0: 2х - 3 = 0 х = 3/2 это точка пересечения с осью х.
3) Исследуем функцию на парность или непарность:
Функция называется парной, если для любого аргумента с его областью обозначения будет f(-x)=f(x), или же непарной - если для любого аргумента с областью обозначения будет f(-x)=-f(x). К тому же, график парной функции будет симметричным относительно оси ординат, а график непарной - симметричным относительно точки (0;0).
Правда, чаще встречается название этих свойств функции как чётность и нечётность.
2*x - 3 -3 - 2*x ---------- = ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет 2*x - 3 -3 - 2*x ---------- = - ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет, значит, функция не является ни чётной, ни нечётной.
4) Исследуем функцию на монотонность: — это значит выяснить, на каких промежутках области определения функция возрастает, а на каких убывает.
Если производная положительна, то функция возрастает и наоборот.
$\frac{d}{dx} ( \frac{2x-3}{4x+5} )= \frac{22}{(4x+5)^2}$ .
Так как переменная в квадрате, то производная всегда положительна, а функция возрастающая на всей числовой оси (кроме х = -5/4).
5) Находим экстремумы функции:
Так как переменная находится в знаменателе, то производная не может быть равна нулю. Следовательно, функция не имеет ни максимума, ни минимума.
6) Исследуем функции на выпуклость, вогнутость:
Если вторая производная меньше нуля, то функция выпуклая, если производная больше нуля - то функция вогнутая.
Вторая производная равна $f''= \frac{-176}{(4x+5)^3}$ .
При x > (-5/4) функция выпуклая, при x < (-5/4) функция вогнута.
7) Находим асимптоты графика функции:
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo 2*x - 3 lim ------- = 1/2 x->-oo4*x + 5 значит,уравнение горизонтальной асимптоты слева:y = 1/2 2*x - 3 lim ------- = 1/2 x->oo4*x + 5 значит,уравнение горизонтальной асимптоты справа:y = 1/2Наклонные асимптотыНаклонную асимптоту можно найти, подсчитав предел функции (2*x - 3)/(4*x + 5), делённой на x при x->+oo и x->-oo 2*x - 3 lim ----------- = 0 x->-oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой справа 2*x - 3 lim ----------- = 0 x->oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой слева
8) Можно найти дополнительные точки и построить график
График и таблица точек приведены в приложении.
1. исследовать функцию и построить график y(x)=(2x-3)/(4x+5) огромная решить , которое выполняется с