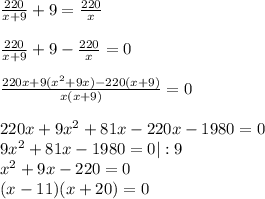
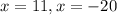
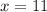
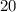
Боковая поверхность конуса = 65π см²
Пошаговое объяснение:
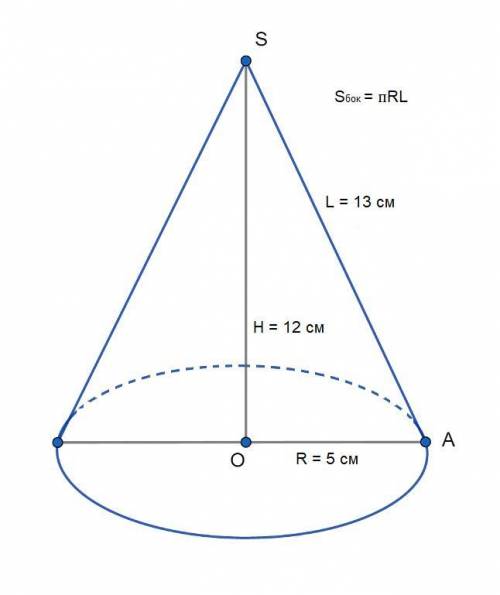
Рисунок прилагается.
Боковая поверхность конуса рассчитывается по формуле S = πRL, R - радиус основания конуса, L - его образующая.
Высота конуса по условию H = SO = 12 см.
Диаметр основания по условию D = 10 см, тогда радиус основания R = D/2 = 10 см / 2 = 5 см.
В прямоугольном треугольнике SOA ∠O = 90°, SA - гипотенуза. Найдем образующую конуса L = SA по т.Пифагора:
SA² = SO² + OA² = 12² + 5² = 144 + 25 = 169 = 13²;
L = SA = 13 см.
Боковая поверхность конуса:
Sбок = πRL = π * 5 * 13 см² = 65π см²
Удобно записать в виде таблицы всевозможные простые числа, отметив при этом участвующие в их записи цифр (картинка). Видно, что цифры 2, 4 и 5 могут участвовать всего в двух числах, причем во всех случаях одно из чисел - вариант ответа.
Предположим, что числа 2 нет в расстановке. Тогда, цифра 2 записывается в составе числа 23. Оставшиеся числа 41 и 5 отлично удовлетворяют условию. Вывод? число 2 может отсутствовать
Предположим, что числа 41 нет в расстановке.Тогда, цифра 4 записывается в составе числа 43. Остались числа 2 и 5. Но цифра 1 осталась незадействованной. Значит, без участия числа 41 такая расстановка невозможна.
ответ: 41
2.
Так как в прямоугольнике нашлась "средняя строка", то в нем нечетное количество строк, но как уточняется больше одной.
Среди делителей числа 40 только два нечетных - число 1 и число 5. Число 1 не подходит по указанным выше причинам. Значит, в прямоугольнике 5 строк, закрашена была 1/5 часть прямоугольника, соответственно число незакрашенных клеток составляет 1-1/5=4/5 часть от общего количества.
ответ: 32