Задание 1.
а) (y - 4)²=у²-2у*4+4²=у²-8у+16;
б) (7x + a)²= (7х)²+2*7х*а+а² = 49х²+14ах+а²;
в) (5с - 1)(5с + 1)=(5с)²-1²;
г) (3а + 2b)(3a - 2b)=(3а)²-(2b)²;
Задание 2.
(а - 9)² - (81 + 2а) = (а²-2×а×9+9²)-81-2а = а²-18а+81-81-2а=а²-20а
Задание 3.
а) x² - 49 = х²-7²=(х-7)(х+7);
б) 25x² - 10xy + y²=(5-у)²;
Задание 4.
(2 - x)² - x (x + 1,5) = 4.
4-4х+х²-х²-1.5х=4
-5.5х=0
х=0
ответ: 0.
Задание 5.
а) (y²- 2a) (2a + y²)=-(у²-2а)²;
б) (3x² + x)²=(9х⁴+6х³+х²);
в) (2 + m)² (2 - m)²=(4+4m+m²)(4-4m+m²).
Задание 6.
а) 4x²y² - 9a⁴=(2ху-3а²)(2ху+3а²);
б) 25а² - (а + 3)²=(5а-а-3)(5а+а+3);
в) 27m³ + n³=(3m)³+n³=(3m+n)(9m²-3mn+n²).
49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =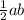 
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника = 
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
б)5.5 ч > 30 мин.
в) 9.9 кг.> 0.3 кг.