Всборнике билетов по всего 60 билетов,в3 из них встречаются вопрос по теме белки. надите вероятность того что в случайно выброном на экзамене билете школьнику достанется вопрос по теме белки
1) Пусть количество джипов=х, тогда после обмена количество джипов сократилось на 10% , т.е. стало 100%-10%=90% =0,9х (90%:100%=0,9) джипов. 2) Количество джипов и спорткаров вначале было поровну, т.е. х. После обмена количество спорткаров увеличилось на 25 %, т.е. стало 100%+25%=125%=1,25х (125%:100%=1,25) спорткаров. 3) Спорткаров стало больше, чем джипов на 14 штук: 1,25х-0,9х=14 0,35х=14 х=40 (спорткаров и 40 джипов было изначально). 4) Посчитаем количество спорткаров после обмена: 1,25х=1,25*40=50 ответ: после обмена у Сидорова стало 50 спорткаров.
Алгоритм решения системы линейных уравнений с двумя неизвестными сложения. 1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях. 2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным 3. Решить полученное уравнение с одним неизвестным и найти одну из переменных. 4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную. 5. Сделать проверку решения.
P = m/n, где n - число все возможных исходов; m - число благоприятных исходов
Число все возможных исходов: n=60
Число благоприятных исходов: m=3.
P = m/n = 3/60 = 0.05
Кому надо такое решение)
Общее число возможных элементарных исходов равно числу которыми можно вынуть билет из 60: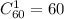
Число исходов, благоприятствующих событию, равно числу которыми можно вынуть билет по теме Белки: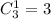
Искомая вероятность: P = 3/60 = 1/20 = 0.05