Пошаговое объяснение:
4) члены геометрической прогрессии
b₁=3к-2
b₂=2к
b₃=к+3
а)
мы знаем, что отношение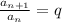 
, составим такие отношения
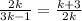⇒ 4k² = (3k-1)(k+3) ⇒ k²-7k+6 =0 ⇒ k₁ = 1; k₂ = 6
b) теперь строим прогрессии
для k₁ = 1 : b₁=3*1-2=1; b₂=2*1=2; b₃=1+3= 4 это возрастающая прогресстя
для k₂ = 6 b₁=3*6-2=16; b₂=2*6=12; b₃=6+3= 9 - это бесконечно убывающая геометрическая прогрессия, ее сумма
, у нас b₁= 16, найдем q= b₂/b₁= 12/16= 0.75, тогда
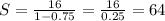
5.
рассуждаем так, в каждом последующем ряду бревен будет на 1 меньше, тогда n-член арифметической прогрессии имеет вид
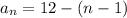, посмотрим, какой ряд будет последним (будет иметь одно бревно)
12-(n-1)=1 ⇒ n=12
найдем сумму 12 членов арифметической прогрессии
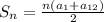
ответ:
) в знаменателе находится многочлен.
2) многочлены находятся и в числителе и в знаменателе.
3) один или оба многочлена могут быть под корнем.
4) многочленов и корней, разумеется, может быть и больше.
пошаговое объяснение:
основные же предпосылки для применения признака даламбера следующие:
1) в общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, , , и так далее. причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
2) в общий член ряда входит факториал. с факториалами мы скрестили шпаги ещё на уроке числовая последовательность и её предел. впрочем, не помешает снова раскинуть скатерть-самобранку:
Берём целую часть. То есть 7.