Іліа́да (дав.-гр. Ἰλιάς, МФА: [iːliás]) — кіклічна поема, що налічує 24 пісні, які складаються з 15693 віршів. Авторство приписують Гомеру. Ця поема є найдавнішою зі збережених пам'яток грецької літератури. «Іліада» є переробкою й об'єднанням численних переказів Стародавньої Греції про подвиги давніх героїв.
Іліада
Ἰλιάς
Helene Paris Louvre K6.jpg
Єлена та Паріс, червонофігурний кратер, анонімний Вазописець із Стокгольма 1999
Жанр
кіклічна поема
Автор
приписується Гомеру
Мова
давньогрецька мова
Написано
8 ст. до н.е.
Попередній твір
Кіпрії
Наступний твір
Ефіопіда і Posthomericad
CMNS: Цей твір у Вікісховищі
Q: Цей твір у Вікіцитатах
Разом з «Одіссеєю» має 8-й номер у Рейтингу 100 найкращих книг усіх часів журналу Ньюсвік[1].
Описано події десятого року облоги Трої (Іліона) об'єднаним військом грецьких вождів. Сказання про попередні події (викрадення Єлени Парісом, виступ греків (ахейців) під верховним начальством Агамемнона), постаті головних вождів (Агамемнон, Менелай, Ахілл, Одісей, Нестор, Діомед, Аякс, Ідоменей та ін., троянський цар Пріам, його сини Гектор, Паріс і т. д.), так само, як і результат війни (загибель Трої), заздалегідь в Іліаді є відомими. Іліада охоплює лише незначний проміжок часу — епізод з історії облоги Трої.
Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
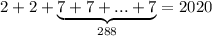
Наибольшим слагаемым является число 7.
ответ: 7