Пошаговое объяснение:
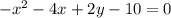
это уравнение кривой второго порядка вида
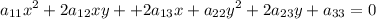
Квадратичная форма B = - x²
Приведем квадратичную форму к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы
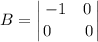
Находим собственные числа и собственные векторы этой матрицы:
(-1 - λ)x + 0*y = 0
0*x + (0 - λ)y = 0
Характеристическое уравнение
λ² + λ = 0
Корни уравнения
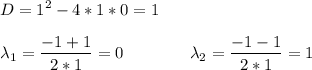
Поскольку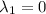 
мы имеем уравнение параболы.
Выделяем полный квадрат
-1(x²+2*2x + 2²) +1*2² = -1(x+2)²+4
Теперь преобразуем уравнение
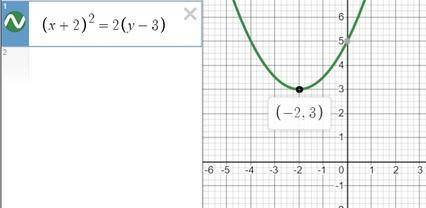
(x+2)² = 2(y-3)
Мы получили канонической вид параболы вида (x-x₀)² = 2p(y-y₀)
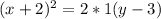это парабола ветвями вверх (p>0), по
направлению оси OY, с вершиной в точке (-2; 3)
