Сначала сократить как обычную дробь. Тут получиться три пары чисел, которые можно сократить: 1,7 и 5,1; 4,92 и 0,82; 7,2 и 4,8. Сокращать можно, если оба числа возможно поделить на одну и ту же цифру (например 1,7 и 5,1 можно поделить на 1,7, то есть получится 1 и 3 соответственно. Теперь, в дроби, вместо 1,7 будет стоять 1, а вместо 5,1 будет 3)
Сокращаем и получаем:
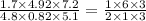
Дальше все числа в числителе и знаменателе перемножаем, чтобы получить только одно число сверху, и только одно снизу:
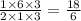
Из получившейся дроби пробуем вынести целое число:
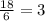
Всё, пример решён, ответ 3
1)От координаты точки У отнимем координаты точки Х, получим длину отрезка ХУ, она равна 12-(-21)=33, т.к. точки М и N делят отрезок ХУ на три равные части, то 33/3=11, координата точки М равна -21+11=-10, а координата точки N равна -10+11=1, и соответственно координата точки У равна 1+11=12, что и дано по условию.
ответ M(-10); N(1)
2) аналогично 1)
От координаты точки У отнимем координаты точки Х, получим длину отрезка ХУ, она равна 24-(-18)=42, т.к. точки М и N делят отрезок ХУ на три равные части, то 42/3=14, координата точки М равна -18+14=-4, а координата точки N равна -4+14=10, и соответственно координата точки У равна 10+14=24, что и дано по условию.
ответ M(-4); N(10)
б) -3,7 + (-6,3 + 2 целых 1/4) = -3,7 + (-6,3) + 2 целых 1/4 = - 10 + 2 целых 1/4 =
= -(10 - 2 целых 1/4) = - (9 целых 4/4 - 2 целых 1/4) = - 7 целых 3/4
в) -(15 целых 2/7 + 4 целых 1/6) + 5 целых 2/7 = -15 целых 2/7 - 4 целых 1/6 + 5 целых 2/7 = (-15 целых 2/7 + 5 целых 2/7) - 4 целых 1/6 = -10 - 4 целых 1/6 =
-14 целых 1/6