Решить можно так:
1). 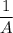 (часть задания) - выполняет первая бригада за 1 день.
(часть задания) - выполняет первая бригада за 1 день.
2). 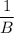 (часть задания) - выполняет вторая бригада за 1 день.
(часть задания) - выполняет вторая бригада за 1 день.
3). 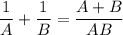 (часть задания) - выполняют две бригады вместе за день.
(часть задания) - выполняют две бригады вместе за день.
4). 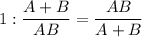 (дней) - выполнят задание обе бригады, если будут работать вместе.
(дней) - выполнят задание обе бригады, если будут работать вместе.
ответ: за 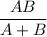 дней.
дней.
Решается очень похоже (только наименования другие):
1). 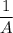 (часть расстояния) - проезжает первый велосипедист за минуту.
(часть расстояния) - проезжает первый велосипедист за минуту.
2). 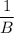 (часть расстояния) - проезжает второй велосипедист за минуту.
(часть расстояния) - проезжает второй велосипедист за минуту.
3). 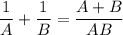 (часть расстояния) - проезжают оба велосипедиста вместе за минуту.
(часть расстояния) - проезжают оба велосипедиста вместе за минуту.
4). 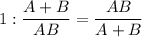 (минут) - встретятся оба велосипедиста, считая от момента начала движения.
(минут) - встретятся оба велосипедиста, считая от момента начала движения.
ответ: через 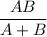 минут.
минут.
Решить можно так:
1). 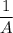 (часть задания) - выполняет первая бригада за 1 день.
(часть задания) - выполняет первая бригада за 1 день.
2). 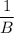 (часть задания) - выполняет вторая бригада за 1 день.
(часть задания) - выполняет вторая бригада за 1 день.
3). 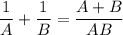 (часть задания) - выполняют две бригады вместе за день.
(часть задания) - выполняют две бригады вместе за день.
4). 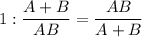 (дней) - выполнят задание обе бригады, если будут работать вместе.
(дней) - выполнят задание обе бригады, если будут работать вместе.
ответ: за 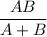 дней.
дней.
Решается очень похоже (только наименования другие):
1). 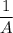 (часть расстояния) - проезжает первый велосипедист за минуту.
(часть расстояния) - проезжает первый велосипедист за минуту.
2). 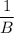 (часть расстояния) - проезжает второй велосипедист за минуту.
(часть расстояния) - проезжает второй велосипедист за минуту.
3). 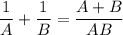 (часть расстояния) - проезжают оба велосипедиста вместе за минуту.
(часть расстояния) - проезжают оба велосипедиста вместе за минуту.
4). 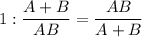 (минут) - встретятся оба велосипедиста, считая от момента начала движения.
(минут) - встретятся оба велосипедиста, считая от момента начала движения.
ответ: через 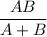 минут.
минут.