Пошаговое объяснение:
ДАНО: y = f(x) = (2-x)*(x+6) = - x² - 4*x + 12
ИССЛЕДОВАНИЕ.
1) Область определения.
Непрерывная, гладкая.
D(f) = R или D(f)∈(-∞;+∞) - ООФ- ответ.
2) Нули функции - пересечение с осью ОХ.
х = -6 и х = 2 - (корни уравнения внутри скобок)
3) Пересечение с осью ОУ.
Y(0) = 12
4) Интервалы знакопостоянства.
Положительна - между нулями.
y>0 при x∈(-6;2)
y≤ 0 при x∈(-∞;-6]∪[2;+∞).
5) Проверка на чётность.
y(-x) = -x² + 4*x+ 12 ≠ y(x). Функция общего вида.
6) Поиск экстремума по первой производной.
y'(x) = -2*x - 4 = 0
x = - 2 - точка экстремума.
7) Локальный экстремум
Максимум: Y(-2) = 16.
8) Интервалы монотонности.
Возрастает: х∈(-∞;-2)
Убывает: х∈(-2;+∞)ю
9) Поиск перегибов по второй производной.
y"(x) = -2. Корней нет.
10) Выпуклая - "горка" во всей ООФ.
11) Область значений: E(f) =(-∞;16)
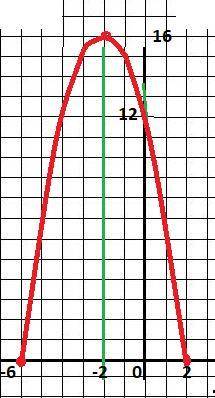
12) Рисунок с графиком в приложении.
Можно (нужно) продолжить и ниже оси ОХ.
15
Пошаговое объяснение:
y=7tgx-7x+15
y'=7·(tgx)'-7·x'+15'
y'=7·1/cos²x -7
y'=7·(1/cos²x -1)=7·(1-cos²x)/cos²x=7·sin²x/cos²x=7·tg²x
y'=7·tg²x
7·tg²x=0
tg²x=0
tgx=0
x=π·n, n∈z
Только при n=0, x=0∈[-пи/4);0]
y(-π/4)=7·tg(-π/4)-7·(-π/4)+15=-7+7π/4+15=8+7·π/4
y(0)=7·tg0-7·0+15=-0-0+15=15
Сравним 8+7·π/4
3<π<3,2⇒ 3/4<π/4<3,2/4⇒ 7·3/4<7·π/4<7·3,2/4⇒5,25<7·π/4<5,6⇒
8+5,25<8+7·π/4<8+5,6⇒13,25<8+7·π/4<13,6⇒8+7·π/4<15⇒15- наибольшее значение функции y=7·tgx-7·x+15 на отрезке [-пи/4;0]
ответ:15
Периметр=8*2+4*2=24(см2)
Площадь=8*4=32(см2)