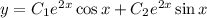Пошаговое объяснение:
1)
1/7*(0,14+2,1-3,5)=1/7*(14/100+21/10-1/7*35/10=1/50+3/10-5/10=1/50+15/50-25/50= -9/50 (или -0,18),
2)
1/12*(4,8-0,24-1,2)=1/12*48/10-24/100-12/10)=1/12*48/10-1/12*24/100-1/12*12/10=4/10-1/50-1/10=20/50-1/50-5/50=14/50=7/25 (или 0,28),
3)
(18 6/7+21 3/4):3=(18+21)+(6/7+3/4): 3=(39+(24/28+21/28): 3=(39+45/28): 3=39: 3+45/28: 3=13+45/28*1/3=13+15/28=13 15/28,
4)
(15 5/7+20 15/16)*1/5=(15+20)+(5/7+15/16)*1/5=(35+(80/112+105/112)*1/5=(35+185/112)*1/5=35*1/5+185/112*1/5=7+37/112=7 37/112
Рівняння вигляду 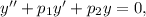 де
де 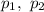 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді 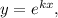 де
де 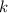 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 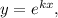 то
то 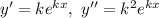
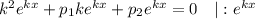
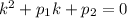 — характеристичне рівняння
— характеристичне рівняння
Можливі три випадки:
➀ 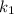 і
і 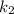 — дійсні,
— дійсні, 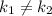
Фундаментальна система розв'язків: 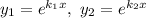 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 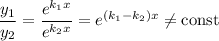
Загальний розв'язок: 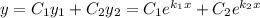
Приклад: а) 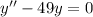
Метод Ейлера: 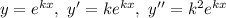
Характеристичне рівняння: 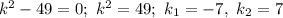
Загальний розв'язок: 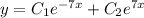
Відповідь: 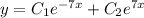
Приклад: в) 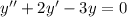
Метод Ейлера: 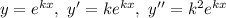
Характеристичне рівняння: 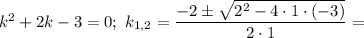
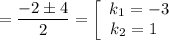
Загальний розв'язок: 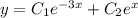
Відповідь: 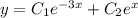
➁ 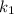 і
і 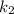 — дійсні,
— дійсні, 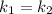
Якщо покласти 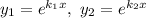 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 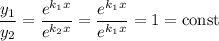
Фундаментальна система розв'язків: 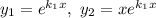 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 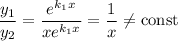
Загальний розв'язок: 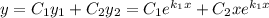
➂ 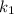 і
і 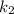 — комплексно спряжені,
— комплексно спряжені, 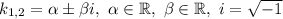
Фундаментальна система розв'язків: 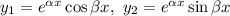 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 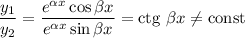
Загальний розв'язок: 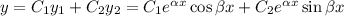
Приклад: б) 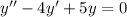
Метод Ейлера: 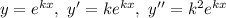
Характеристичне рівняння: 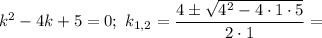
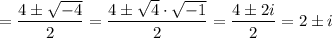
Отже, 
Загальний розв'язок: 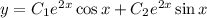
Відповідь: