Площадью круга называется предел площадей правильных вписанных многоугольников при бесконечном удвоении числа их сторон.
Пошаговое объяснение:
Важно:
•Замкнутая кривая (линия), чьи точки лежат на одинаковом расстоянии от одной точки её центра, называется окружностью.
•Окружность разбивает плоскость на две области: внутреннюю и внешнюю.
Важно:
•Та часть плоскости, которая лежит внутри окружности (вместе с самой окружностью) называется кругом.
•окружность — это замкнутая линия ( граница круга).
•круг — это внутренняя область окружности.
•У окружности нельзя посчитать площадь! А у круга найти площадь, зная формулу, достаточно легко.
Для расчета площади круга используется формула:
S = πR2, где R — радиус круга,
S = π (D/2)^2 = π D^2/2^2 = π D^2/4
где D — диаметр круга, т.к. R = D/2
5 см
Пошаговое объяснение:
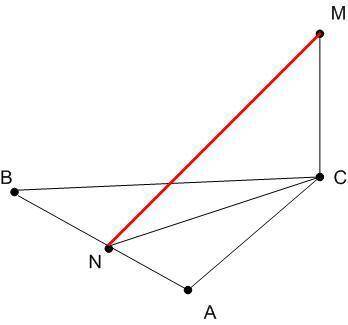
IACI=IBCI по условию, как стороны равнобедренного треугольника.
Построим отрезок СN такой, что IANI=IBNI. Отрезок CN является одновременно медианой, высотой и биссектрисой, опущенной на основание равнобедренного треугольника. Следовательно ∠CNA = ∠CNB = 90° (по определению высоты, опущенной из вершины на основание), и IANI=IBNI (по определению медианы).
Плоскость ΔMNC перпендикулярна отрезку AB, т.к. AB ⊥CN (определение: прямая перпендиклярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости), следователно и MN ⊥ AB.
Следовательно длина отрезка IMNI и есть расстояние от точки M до стороны (отрезка) AB (определение: расстояние от точки до плоскости есть длина перпендикуляра, опущенного из точки на плоскость).
Найдем длину отрезка MN:
1. Сначала найдем длину ICNI:
ICNI=√(IBCI² - INBI²);
ICNI=√(5²-4²)=√9=3;
2. А теперь найдем IMNI из ΔMNC:
IMNI=√(ICNI²+ICMI²);
IMNI=√(3²+4²)=√25=5 (см)
волНы
опАсность