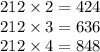
Рассуждения в разделе "Пошаговое объяснение".
Пошаговое объяснение:Признаки делимости числа на 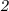 :
:
Число делится на  , если его конечная цифра чётная.
, если его конечная цифра чётная.
Пример: 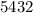 делится на
делится на  , ибо его конечная цифра чётная.
, ибо его конечная цифра чётная.
Признаки делимости числа на 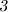 :
:
Число делится на  , если сумма его цифр делится на
, если сумма его цифр делится на  .
.
Пример: 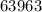 делится на
делится на  , ибо сумма его цифр делится на
, ибо сумма его цифр делится на  .
.
Признаки делимости числа на 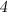 :
:
Число делится на  , если его
, если его  последние цифры нули или образуют число, делящиеся на
последние цифры нули или образуют число, делящиеся на  .
.
Пример: 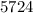 делится на
делится на  , ибо
, ибо  последние цифры (последняя цифра, если число однозначное) образуют число
последние цифры (последняя цифра, если число однозначное) образуют число 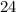 , делящиеся на
, делящиеся на  .
.
Признаки делимости числа на 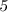 :
:
Число делится на  , если его конечная цифра
, если его конечная цифра 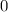 или
или  .
.
Пример: 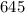 делится на
делится на  , ибо его конечная цифра
, ибо его конечная цифра  .
.
Признаки делимости числа на 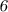 :
:
Число делится на 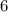 , если конечная цифра чётная и сумма цифр этого числа делится на
, если конечная цифра чётная и сумма цифр этого числа делится на  .
.
Пример: 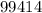 делится на
делится на 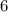 , ибо его конечная цифра
, ибо его конечная цифра  чётная и сумма цифр этого числа делится на
чётная и сумма цифр этого числа делится на  .
.
Признаки делимости числа на 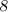 :
:
Число делится на 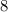 , если
, если  его последние цифры образуют число, делящиеся на
его последние цифры образуют число, делящиеся на 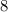 .
.
Пример: 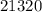 делится на
делится на 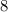 , ибо
, ибо  его последние цифры образуют число
его последние цифры образуют число 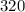 , делящиеся на
, делящиеся на 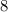 .
.
Признаки делимости числа на 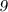 :
:
Число делится на 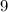 , если сумма его цифр делится на
, если сумма его цифр делится на 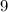 .
.
Пример: 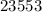 делится на
делится на 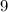 , ибо сумма его цифр делится на
, ибо сумма его цифр делится на 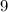 .
.
Признаки делимости числа на  :
:
Число делится на 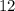 , если оно кратно
, если оно кратно  и
и  .
.
Пример: 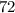 делится на
делится на 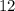 , ибо оно кратно
, ибо оно кратно  и
и  .
.
Признаки делимости числа на 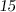 :
:
Число делится на 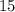 , если его конечная цифра
, если его конечная цифра 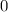 или
или  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
Пример: 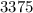 делится на
делится на 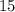 , ибо его конечная цифра
, ибо его конечная цифра  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
------------------------------------------------------------------------------------------------
Какие из чисел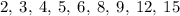 являются делителем
являются делителем 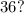
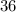 делится на
делится на 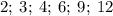 , ибо его конечная цифра чётная, сумма цифр этого числа делится на
, ибо его конечная цифра чётная, сумма цифр этого числа делится на  и
и 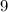 , оно кратно
, оно кратно  и
и  , его
, его  последние цифры образуют число, делящиеся на
последние цифры образуют число, делящиеся на  .
.
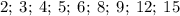 являются кратным
являются кратным 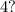
Справедливо неравенство: 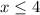 .
.
Числа 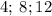 кратны
кратны  , ибо последняя цифра
, ибо последняя цифра 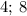 делится/
делится/ последние цифры
последние цифры 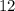 делятся на
делятся на  .
.
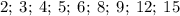 являются делителем
являются делителем 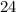 и
и 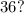
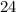 и
и 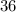 одновременно делятся на
одновременно делятся на 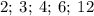 , ибо их конечные цифры чётные, суммы цифр этих чисел делятся на
, ибо их конечные цифры чётные, суммы цифр этих чисел делятся на  , их
, их  последние цифры образуют числа, делящиеся на
последние цифры образуют числа, делящиеся на  .
.
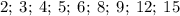 являются делителем
являются делителем 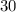 и кратным
и кратным 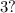
Требования к заданию: 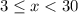 , где
, где  - искомые числа. Число
- искомые числа. Число  уже не подходит.
уже не подходит.
Числа 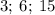 являются делителями
являются делителями 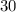 и кратны
и кратны  , ибо сумма цифр числа
, ибо сумма цифр числа 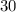 делится на
делится на  , последняя цифра
, последняя цифра 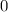 и она чётная.
и она чётная.
ответ: 1000 - наименьшее; 9 990 - наибольшее ( числа делятся и на 2 и на 5)
Пояснения:
-число делится на 2, если оканчивается на 0; 2; 4; 6; 8
-число делится на 5, если его последняя цифра 0 или 5
значит, чтобы число делилось и на 2 и на 5, его последняя цифра должны быть 0
наименьшее четырехзначное число - это 1 000 ( по признакам делимости делится и на 2 и на 5)
наибольшее четырехзначное число - это 9 999 ( но нам нужна последняя цифра 0)
значит, наибольшее четырехзначное число, которое делится и на 2 и на 5 - это 9 990
212*3=636
212*4=848
Задача.
Шаг сына составляет 1/2 шага отца. Значит, шаг сына 40 см. 5*40=200см
в каждом метре 100 см
ответ: 2 метра