18
Пошаговое объяснение:
уравнение касательной
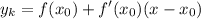
у нас 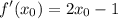
запишем наше уравнение касательной
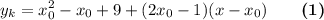
теперь мы знаем, что касательная должна проходить через точку (0;0),
т.е. 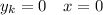
подставим это в уравнение касательной

решим это уравнение относительно х₀
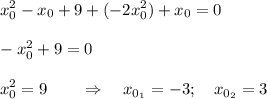
итак, у нас есть две точки касания, касательные в которых проходят через точку (0; 0). но по условию нам нужна только точка с положительной абсциссой, поэтому наше решение х₀ = 3 и точка имеет координаты
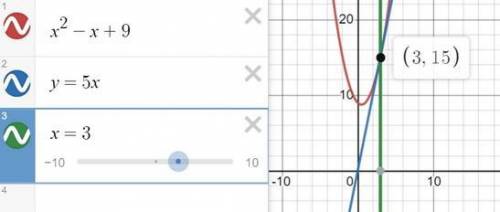
f(3) = 3² -3 +9 = 15 и тогда точка (3; 15)
и тогда сумма координат 3 +15 = 18 - это уже ответ.
но мы дополнительно найдем уравнение касательной, чтобы проверить наш ответ
подставим это значение в уравнение касательной (1)
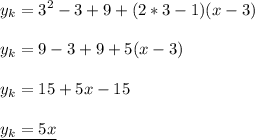
это и есть уравнение касательной с положительной абсциссой и проходящей через начало координат
и тогда наш
ответ
3 + 15 = 18
Пошаговое объяснение:
y' - 4xy = x. => y' = (4y + 1)x.
Разделяем переменные:
dy/dx = (4y + 1)x => dy/(4y + 1) = xdx.
(Везде далее фигурные скобки будут означать модуль) Интегрируем обе части и получаем:
(1/4)ln{4y + 1} = x^2/2 + C.
Это можно выразить явно для y:
y = (exp(2x^2 + C) - 1)/4, где C - другая произвольная постоянная.
Подставляем начальные условия:
3/4 = (exp(C) - 1)/4 => exp(C) - 1 = 3, C = ln 4.
Тогда частное решение можно будет записать как:
y = (4exp(2x^2) - 1)/4 = exp(2x^2) - 1/4.
х+х-2+х+1=11
3х=11+2-1
3х=12
х=12:3
х=4 шарика у Даши
сколько шариков у Маши
4-2=2 шарика
сколько шариков у Саши
4+1=5 шариков