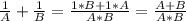Факторизация числа:
1792 = 7 * 2^8
Пусть А и 2*А - наименьшее и наибольшее числа.
Видно, что они не делятся на 7, иначе произведение делилось бы на 7^2.
Поэтому А - степень двойки. Перебираем:
1) А = 1, ну это явно не то
2) А = 2, тоже не айс
3) А = 4. Между 4 и 8 есть число 7, и можно взять числа 4,7,8,8, произведение которых суть 1792.
4) А = 8. Между 8 и 16 возьмем число, деляшееся на 7, это 14. И как раз 8*14*16 = 1792.
5) А = 16. Это уже слишком много т. к. 16*32 содержит в себе 9 двоек, а у нас только 8.
Итого 2 варианта.
Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1) 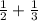
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
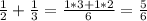
2) 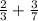
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
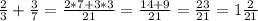
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3) 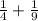
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
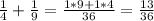
2) 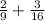
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
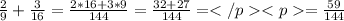
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.