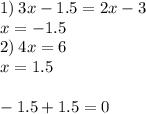
 , если
, если 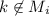 и
и 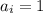 , если
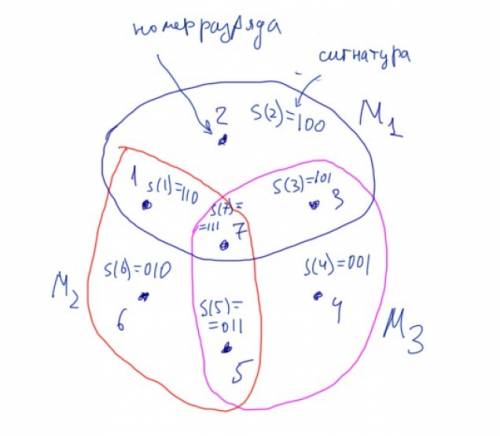
, если 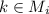 , где i=1,2,3. Назовем эту тройку сигнатурой разряда. Если для каких то двух разрядов c номерами k и m оказалось s(k)=s(m), то у Игоря нет никакой принципиальной возможности определить какая цифра в какой позиции находится. Поэтому количество цифр, которое может определить Игорь за 3 хода, не превосходит количества различных троек s(k), т.е. не превосходит 2³=8, и значит N≤8. И если Игорь хочет определять своими ходами максимальное количество разрядов, то ходы ему надо составлять так, чтобы каждой сигнатуре принадлежал только один разряд. и M₁∪M₂∪M₃ охватывало как можно больше разрядов. Если для какого-то разряда его сигнатура оказалась (0,0,0), т.е. этот разряд вообще не был затронут ходами Игоря, то определить цифру в этом разряде невозможно, т.к. цифр всего 10 и 10>8. Т.е. Игорь может определять цифры только в тех разрядах, которые принадлежат M₁∪M₂∪M₃. Значит N≤7. Покажем, что при N=7 множества M₁, M₂ и M₃ можно выбрать так, что каждой сигнатуре будет принадлежать только один разряд, и значит 7 цифр Игорь сможет всегда определить, например, с следующих ходов:
, где i=1,2,3. Назовем эту тройку сигнатурой разряда. Если для каких то двух разрядов c номерами k и m оказалось s(k)=s(m), то у Игоря нет никакой принципиальной возможности определить какая цифра в какой позиции находится. Поэтому количество цифр, которое может определить Игорь за 3 хода, не превосходит количества различных троек s(k), т.е. не превосходит 2³=8, и значит N≤8. И если Игорь хочет определять своими ходами максимальное количество разрядов, то ходы ему надо составлять так, чтобы каждой сигнатуре принадлежал только один разряд. и M₁∪M₂∪M₃ охватывало как можно больше разрядов. Если для какого-то разряда его сигнатура оказалась (0,0,0), т.е. этот разряд вообще не был затронут ходами Игоря, то определить цифру в этом разряде невозможно, т.к. цифр всего 10 и 10>8. Т.е. Игорь может определять цифры только в тех разрядах, которые принадлежат M₁∪M₂∪M₃. Значит N≤7. Покажем, что при N=7 множества M₁, M₂ и M₃ можно выбрать так, что каждой сигнатуре будет принадлежать только один разряд, и значит 7 цифр Игорь сможет всегда определить, например, с следующих ходов: