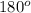 или
или 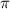 Рассмотрим рисунокКак видно, четирехугольники ABLK и ABMN есть вписанными в окружности ( все их вершины по определению лежат на окружностях). Поэтому можна сказать что сумма углов AKL и ABL равна 180. А постольку углы ABL и ABN являются смежными, то их сумма тоже равна 180. С этого можна сделать вывод, что углы AKL и ABN равны. Дальше аналогично можна показать что углы PMN и ABN (P - точка на прямой KM) равны, а поскольку если две прямых отсекают на третьей одинаковые углы, то они паралельны, то с этого можна сделать вывод что KL и MN паралельны.
Рассмотрим рисунокКак видно, четирехугольники ABLK и ABMN есть вписанными в окружности ( все их вершины по определению лежат на окружностях). Поэтому можна сказать что сумма углов AKL и ABL равна 180. А постольку углы ABL и ABN являются смежными, то их сумма тоже равна 180. С этого можна сделать вывод, что углы AKL и ABN равны. Дальше аналогично можна показать что углы PMN и ABN (P - точка на прямой KM) равны, а поскольку если две прямых отсекают на третьей одинаковые углы, то они паралельны, то с этого можна сделать вывод что KL и MN паралельны.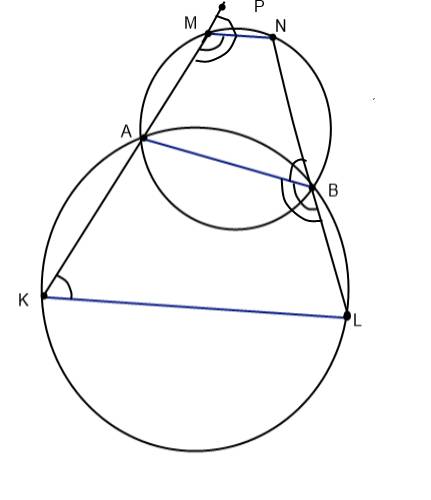
Но это невозможно. Если 1 взял два больших, а 2 взял 3 маленьких, то
19+23=42 < 13+15+16=44
Значит, тот кто взял больше, взял 3 ящика, а второй 2 ящика.
Первый взял вдвое больше второго, то есть чётное число.
Значит, он взял 2 нечетных ящика и 1 чётный. Проверим.
1) 19+23+18=60, но 30 кг из 2 ящиков сложить нельзя.
Можно только 13+16=29 или 15+16=31.
2) 19+23+16=58, но 29 кг тоже сложить нельзя, только 13+15=28.
3) 15+23+18=56, но 28 тоже не получается, только 13+16=29.
4) 15+23+16=54, но 27 получить нельзя.
5) 13+23+18=54, но 27 опять получить нельзя.
6) 13+23+16=52, но 26 тоже не получается.
Без ящика 23 кг совсем ничего не получится, дальше проверять смысла нет.
Итак, я пришёл к выводу, что такой набор нельзя разбить так, как надо.