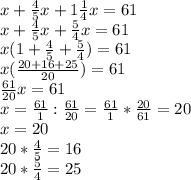
Дана функция f(x) = -2x³ - 7x² - 36.
Находим её производную: y ' = -6x² - 14x.
Приравняем производную нулю: -6x² - 14x = -2x(3x + 7) = 0.
Отсюда определяем критические точки: х1 = 0 и х2 = (-7/3).
Выясняем характер этих точек по знакам производной левее и правее точки.
x = -3 -7/3 -1 0 1
y' = -12 0 8 0 -20.
Имеем 3 промежутка монотонности функции:
(-∞; (-7/3)), ((-7/3); 0), (0; +∞).
Где производная положительна - там функция возрастает: ((-7/3); 0),
где производная отрицательна - там функия убывает: (-∞; (-7/3)), (0; +∞).
6sin²(x) - 5cos(x) - 5 = 0
6 • (1 - cos²(x)) - 5cos(x) - 5 = 0
6 - 6cos²(x) - 5cos(x) - 5 = 0
-6cos²(x) - 5cos(x) + 1 = 0
• Пусть cos(x) = t, тогда cos²(x) = t², причём: | t | ≤ 1
-6t² - 5t + 1 = 0 / • (-1)
6t² + 5t - 1 = 0
(a = 6, b = 5, c = -1)
D = b² - 4ac
D = 5² - 4 • 6 • (-1) = 25 + 24 = 49 = 7²
t₁,₂ = (-b ± √D)/2a
t₁ = (-5 + 7)/2 • 6 = 2/12 = ⅙
t₂ = (-5 - 7)/2 • 6 = -12/12 = -1
• Оба значения подходят под наше условие: | t | ≤ 1, поэтому получаем систему:
[ cos(x) = ⅙
[ cos(x) = -1
[ x₁ = ± arccos(⅙) + 2πn, n ∈ ℤ
[ x₂ = π + 2πn, n ∈ ℤ
x₁ = ± arccos(⅙) + 2πn, n ∈ ℤ
x₂ = π + 2πn, n ∈ ℤ
4/5*х + 1 1/4*х + х = 61
4/5*х + 5/4*х + х = 61
16/20*х + 25/20*х + х = 61
41/20*х + х = 61
41/20*х + 20/20*х = 61
61/20*х = 61
х = 61 : 61/20
х = 61 * 20/61
х = 20 => длина третьей стороны -- 20 см, второй - 20*5/4 = 25 см, первой -- 20 * 4/5 = 16 см.